Introdução à Modelos Estatísticos no R

Análise de dados univariados
Teste t

Maurício Vancine

15 de maio de 2023

Maurício Vancine

• Ecólogo (2014)

• Doutorando em Ecologia (2020-2024)

• Ecologia Espacial

• Modelagem Ecológica

• Análise de Dados Geoespaciais

• Ecologia e Conservação de Anfíbios

• Open source [R, QGIS, GRASS GIS, GNU/Linux, …]

Análises Ecológicas no R (2022)

• 15 capítulos: perguntas em ecologia, linguagem R, tidyverse, análises univariadas, multivariadas e geoespaciais

• bookdown

• PDF

• Amazon

• Código Fonte

• YouTube

Conteúdo

Tempo: 2 horas

1. Linguagem R (30 min.)
2. Análise exploratória de dados (30 min.)
3. Análise de dados multivariados (60 min.)

IMPORTANTE!!!

Estamos num espaço seguro e amigável

Sintam-se à vontade para me interromper e tirar dúvidas

1. Linguagem R

Definição

O R é uma linguagem de programação livre (open source), direcionada à manipulação, análise e visualização de dados, com diversas expansões (pacotes) para dados ou análises específicas

Histórico - Linguagem S

John M. Chambers (Stanford University, CA, EUA)

Versões

• Old S (1976-1987)
• New S (1988-1997)
• S4 (1998)

IDE (Integrated Development Environment)

• Interface: S-PLUS (1988-2008)

Histórico - Linguagem R

Robert Gentleman e Ross Ihaka (Auckland University, NZ)

Versões

• Desenvolvimento (1993-2000)
• Versão 1 (2000-2004)
• Versão 2 (2004-2013)
• Versão 3 (2013-2020)
• Versão 4 (2020-atual)

IDE (Integrated Development Environment)

• Interface: RStudio (2011-atual)
• Atualmente: R Core Team

Histórico - Linguagem R

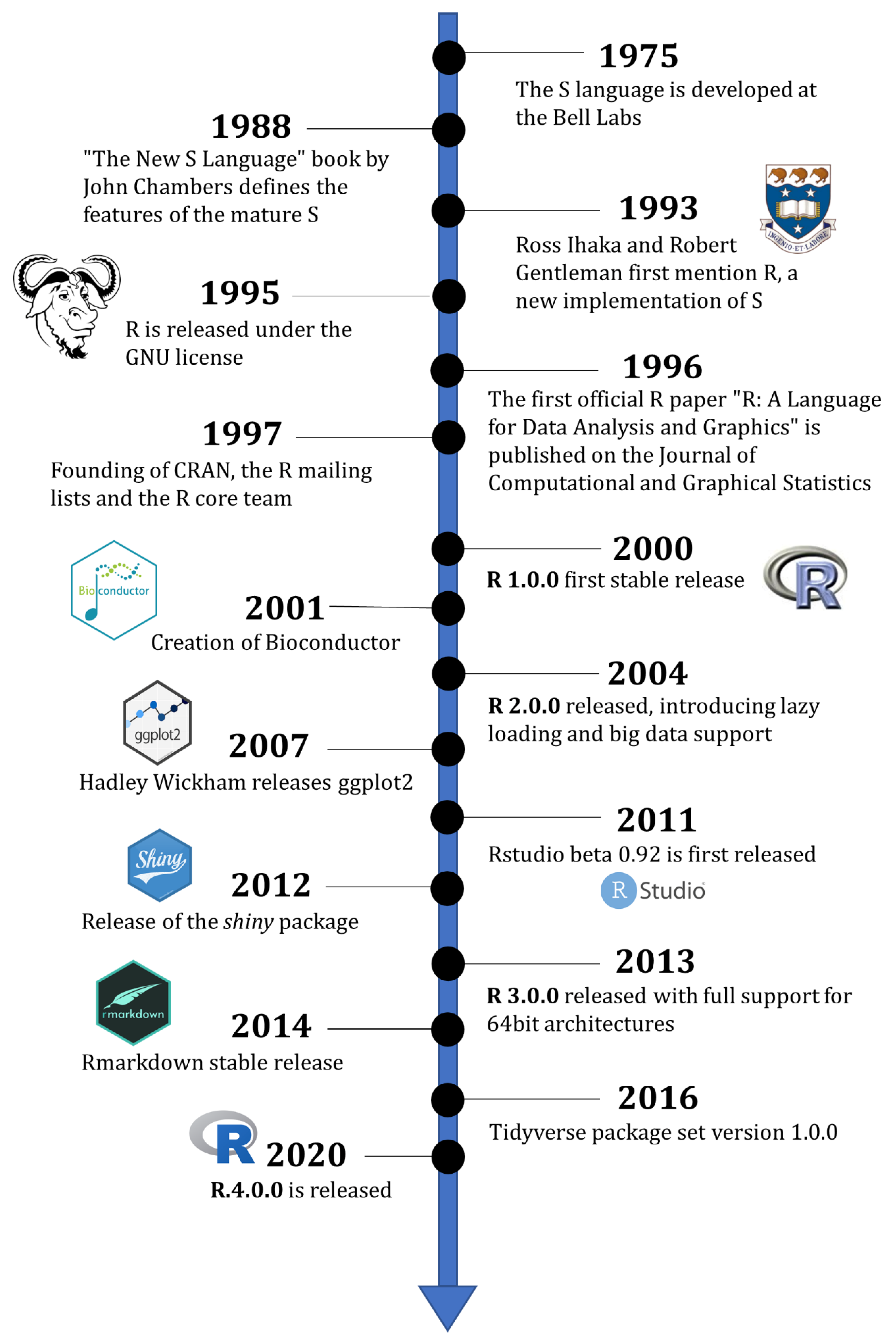
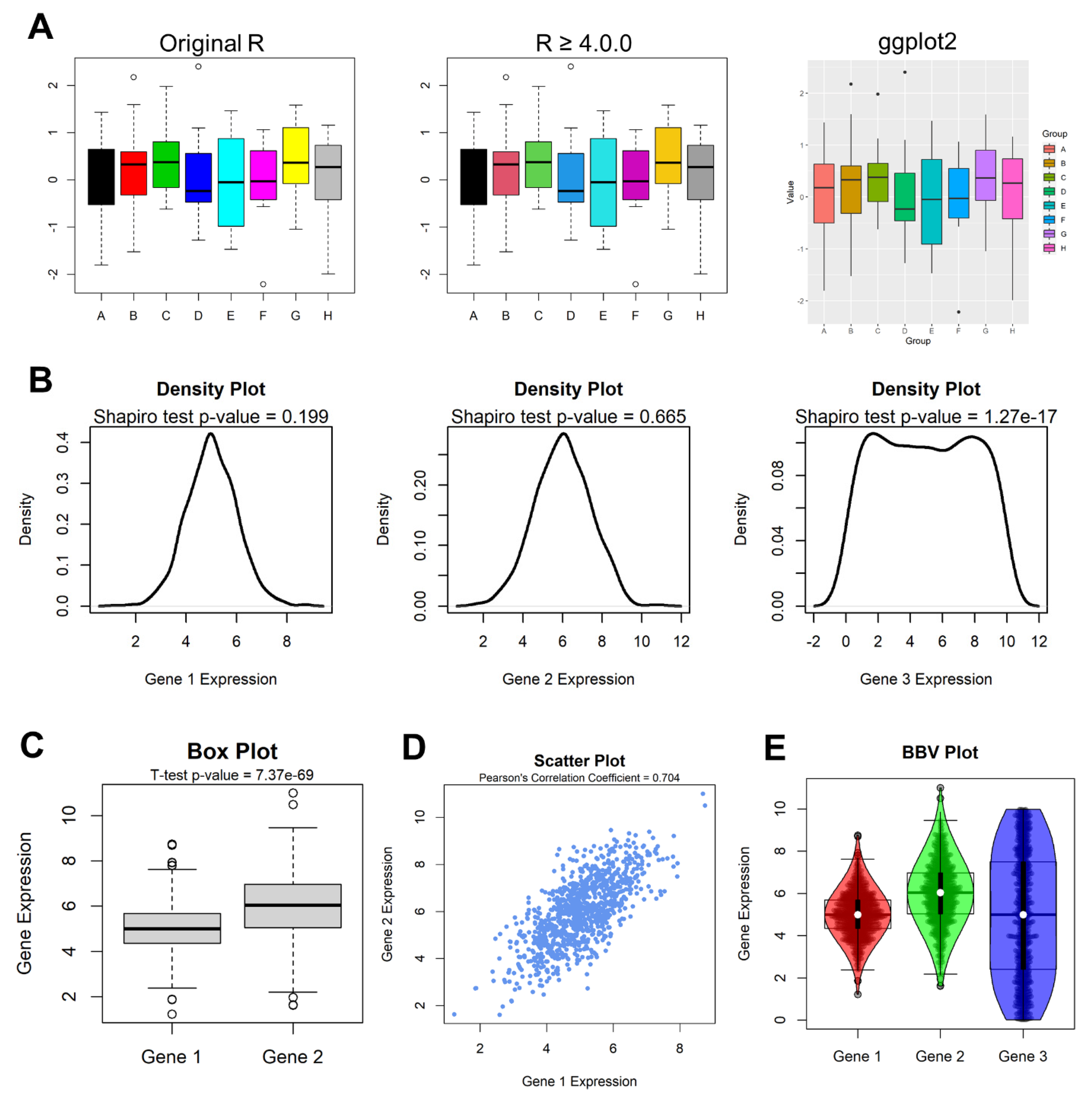
Aplicações

Manipulação, visualização e análise de dados

• Estatísticas univariadas e multivariadas
• Análises de dados ecológicos
• Análise de dados espaciais, temporais e sonoros
• Análise de dados funcionais, genéticos e filogenéticos
• Análise de dados geoespaciais e sensoriamento remoto
• Visualização de todos os tipos de dados anteriores

R Markdown e quarto

• Textos em HTML, PDF, Word, ODT, Markdown
• Slides, Websites, Blogs, Livros e Artigos
• Shiny

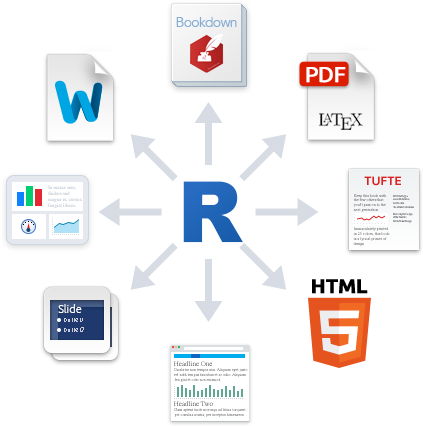
IDE

Ambiente de Desenvolvimento Integrado (Integrated Development Environment)

IDE

Ambiente de Desenvolvimento Integrado (Integrated Development Environment)

Interface

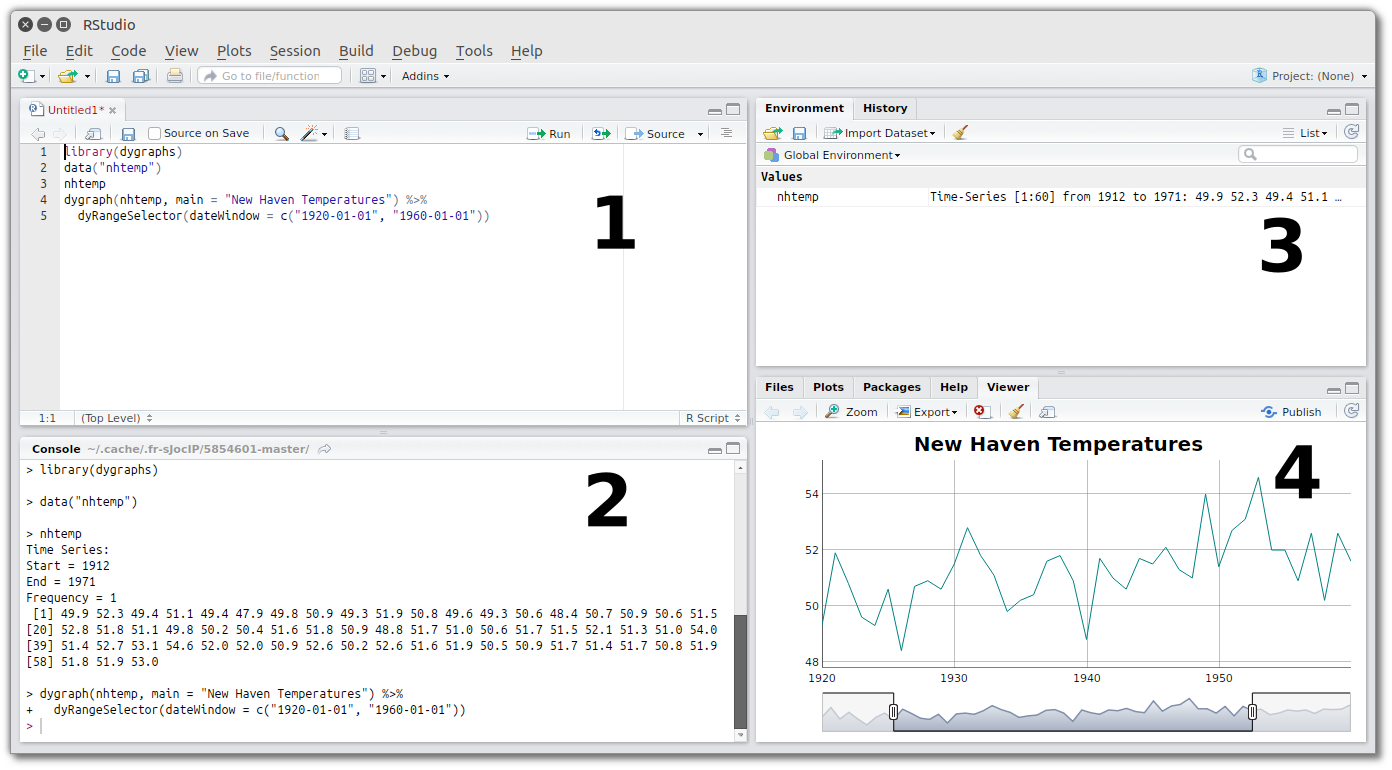
Projeto R (.Rproj)

• Facilita o trabalho em múltiplos ambientes
• Cada projeto possui seu diretório, documentos e workspace
• Permite controle de versão (git e GitHub)

Antes de começarmos…

Conferindo os computadores

Console

O console é onde a linguagem R instalada é carregada para executar os códigos

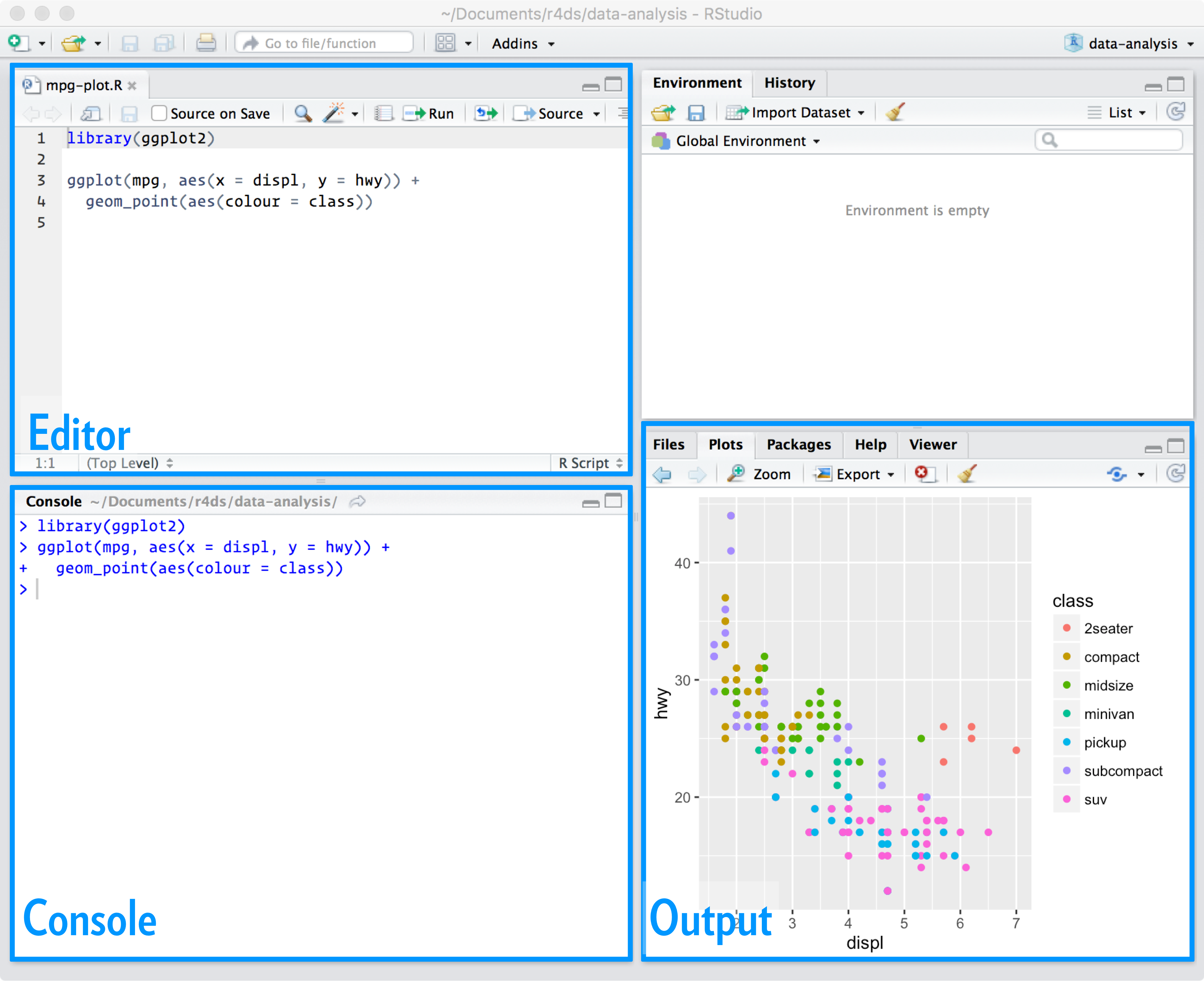
Console

• Na janela do console aparece o símbolo >, seguido de uma barra vertical | que fica piscando (cursor), onde digitamos ou enviamos nossos códigos do script

• Vamos digitar 10 + 2 e apertar a tecla Enter para que essa operação seja executada

• O resultado retorna o valor 12, precedido do valor 1 entre colchetes [1]

10 + 2

[1] 12

Console

• Os colchetes [] demonstram a posição do elemento numa sequência de valores

• Vamos criar uma sequência usando o operador : para demonstrar isso

• O número que aparecer nos colchetes vai depender da largura das janelas

1:42

 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
[26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42

Console

Noções de programação

Número inteiro (integer)

1

[1] 1

Número decimal (float ou double)

1.2

[1] 1.2

Texto entre aspas simples ('') ou duplas ("") (character ou string)

"Este é o número 1"

[1] "Este é o número 1"

Lógico (letras maiúsculas) (booleano)

TRUE

[1] TRUE

FALSE

[1] FALSE

Script

Onde os códigos são escritos e salvos no formato .R

• Atalho: ctrl + shift + N

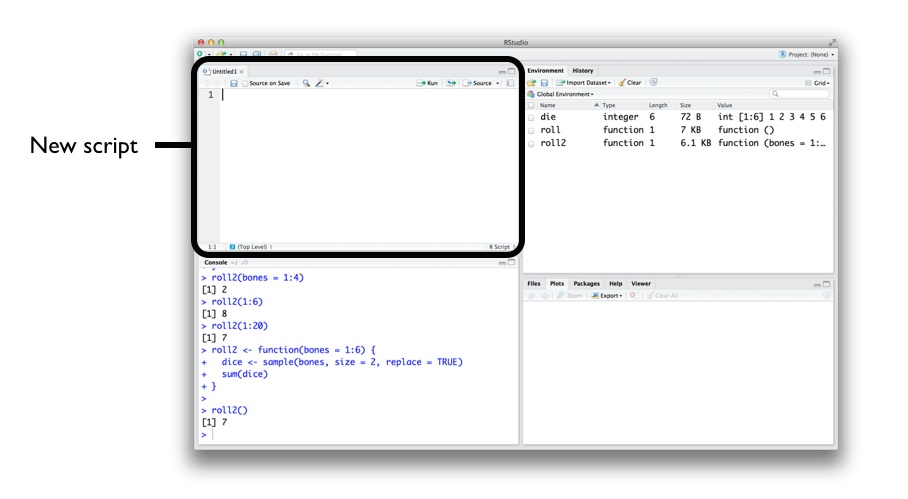
Script

• Os códigos devem ser digitados preferencialmente no script

• Para executar um código, deixem o cursor em qualquer lugar da linha

• Atalho: ctrl + enter

1

[1] 1

1 + 2

[1] 3

Script

Salvar um script

• Atalho: ctrl + S

Script

Comentários (#)

• Comentários não são lidos pelo R e descrevem informações em nosso script

• São representados pelo # (hash) ou #' (hash-linha)

# comentarios
# o r nao le o codigo depois do # (hash)

42 # essas palavras nao sao executadas, apenas o 42

[1] 42

Script

Comentários (#)

• Sempre comece um script com um cabeçalho

• Ajuda a lembrar o que o script faz e quando foi escrito

#' ----
#' título: modelos estatisticos em ecologia
#' autor: seu nome
#' data: 2023-04-26
#' ----

Operadores

Operadores aritméticos (retorna números)

Operador	Descrição	Uso
+	Adição	a + b
–	Subtração	a - b
*	Multiplicação	a * b
/	Divisão	a / b
%%	Resto da divisão	a %% b
%/%	Quociente da divisão	a %/% b
^	Potenciação	a^b

Operadores

Operadores relacionais (retorna TRUE|FALSE)

Operador	Descrição	Uso
<	Menor	a < b
>	Maior	a > b
<=	Menor ou igual	a <= b
>=	Maior ou igual	a > = b
==	Igual	a == b
!=	Não igual (diferente)	a!=b

Operadores

Ordem das operações aritméticas

() > ^ > * ou / > + ou -

# sem especificar - segue a ordem das operações
1 * 2 + 2 / 2 ^ 2

[1] 2.5

# especificando - segue a ordem dos parênteses
((1 * 2) + (2 / 2)) ^ 2

[1] 9

Objetos

Palavras que atribuímos (guardamos) dados possibilitando sua manipulação

• Atribuição (<-)

• palavra <- dados

• Atalho: alt + -

Objetos

Vamos atribuir o valor 10 à palavra eco

# atribuicao - simbolo (<-)
eco <- 10 

Objetos

• Sempre confira a atribuição

• Dica: chame o objeto novamente

# atribuicao - simbolo (<-)
eco <- 10 
eco

[1] 10

Objetos

Seja criativo

O R sobrescreve os valores dos objetos com o mesmo nome

# eco vale 10
eco <- 10 
eco

[1] 10

# agora eco vale 2
eco <- 2 
eco

[1] 2

Objetos

Seja criativo, mas nem tanto…

O R tem limitações ao nomear objetos!

1. Começar por letras (a-z ou A-Z) ou pontos (.)

2. Conter letras (a-z ou A-Z), números (0-9), underscores (_) ou pontos (.)

3. Case-sensitive, i.e., ele difere letras maiúsculas de minúsculas

4. Evitar utilizar letras maiúsculas, acentos ou cedilha (ç)

5. Não podem ser iguais a nomes especiais: break, else, FALSE, for, function, if, Inf, NA, NaN, next, repeat, return, TRUE, while

for <- 1

Error: <text>:1:5: unexpected assignment
1: for <-
        ^

Objetos

Ambiente (Environment)

Os objetos podem ser visualizados no painel Environment

Objetos

Podemos utilizar objetos para fazer operações

# definir dois objetos
eco1 <- 10
eco2 <- 2

# operacoes com objetos
eco1 + eco2 # adicao

[1] 12

eco1 - eco2 # subtracao

[1] 8

eco1 * eco2 # multiplicacao

[1] 20

eco1 / eco2 # divisao

[1] 5

Objetos

Podemos utilizar objetos para atribuir resultados de operações

# operacoes com objetos e atribuicao
adi <- eco1 + eco2 # adicao
adi

[1] 12

sub <- eco1 - eco2 # subtracao
sub

[1] 8

mul <- eco1 * eco2 # multiplicacao
mul

[1] 20

div <- eco1 / eco2 # divisao
div

[1] 5

Objetos

Tipos de objetos

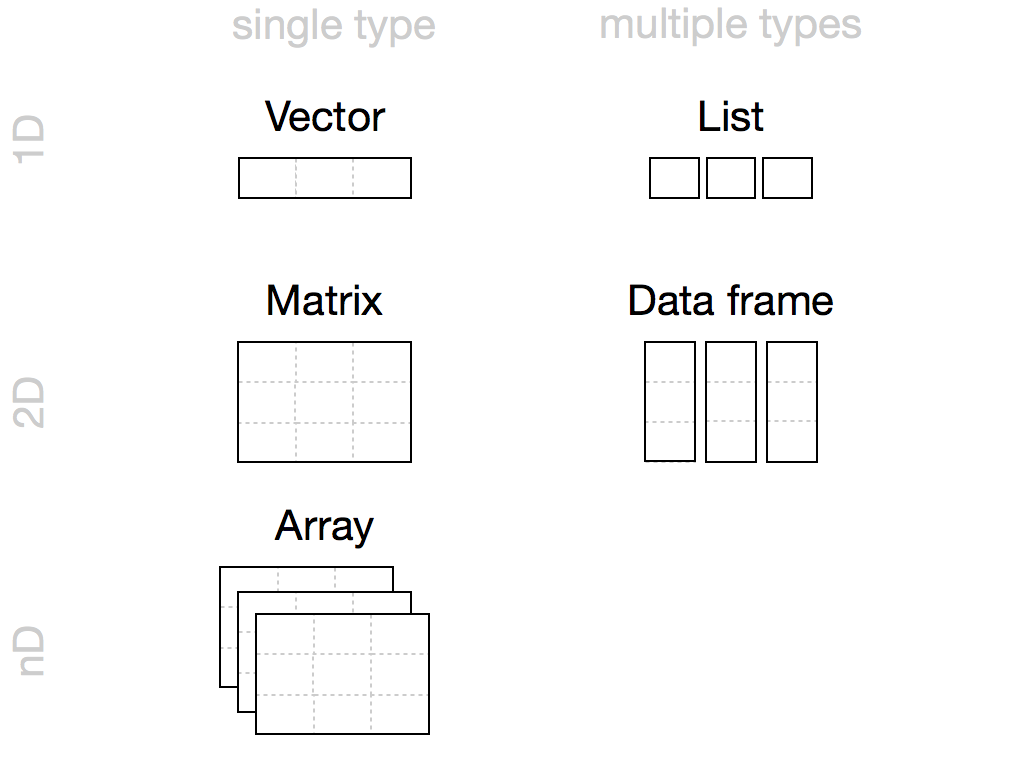
Funções

Códigos que realizam operações em argumentos

• Estrutura de uma função:

nome_da_funcao(argumento1, argumento2)

1. Nome da função: remete ao que ela faz (inglês)
2. Parênteses: limitam a função
3. Argumentos: onde a função atuará
4. Vírgulas: separam os argumentos

Funções

Exemplos

# soma
sum(10, 2)

[1] 12

# soma de objetos
sum(eco1, eco2)

[1] 12

# soma de objetos atribuidos a objetos
eco_sum <- sum(eco1, eco2)
eco_sum

[1] 12

Funções

Argumentos

Os argumentos podem ser de dois tipos:

1. Objetos ou valores: dados onde a função irá atuar

2. Parâmetros: mudam o comportamento da função (texto = TRUE, FALSE ou "texto")

sum(1, 2, 3, NA)

[1] NA

sum(1, 2, 3, NA, na.rm = TRUE)

[1] 6

Funções

Argumentos como valores

# funcoes - argumentos como valores
sum(10, 2)

[1] 12

prod(10, 2)

[1] 20

Argumentos como objetos

# funcoes - argumentos como objetos
sum(eco1, eco2)

[1] 12

prod(eco1, eco2)

[1] 20

Funções

Argumentos como parâmetros

# repeticao - vezes
rep(x = 1:5, times = 5)

 [1] 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

# repeticao - cada
rep(x = 1:5, each = 5)

 [1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5

Funções

Atribuição de resultados a objetos

# atribuicao dos resultados
rep_times <- rep(x = 1:5, times = 5)
rep_times

 [1] 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

rep_each <- rep(x = 1:5, each = 5)
rep_each

 [1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 4 4 4 4 4 5 5 5 5 5

Funções

Atribuição, função e linha temporal

Criar dois objetos

# criar dois objetos
foo <- 2
bar <- 3

Somar esses objetos e atribuição

# somar e atribuir
su <- sum(foo, bar)
su

[1] 5

Raiz quadrada e atribuição

# raiz e atribuir
sq <- sqrt(su)
sq

[1] 2.236068

Funções

Atribuição, função e linha temporal

1. Atribuição de dados a objetos

2. Funções que operam e mudam esses dados

3. Nova atribuição desses resultados a novos objetos

# criar dois objetos
foo <- 2
bar <- 3

# somar e atribuir
su <- sum(foo, bar)

# raiz e atribuir
sq <- sqrt(su)

Ajuda

Descreve as informações de uma função

# descreve as informacoes de uma funcao
help("mean") # arquivo .html
?mean

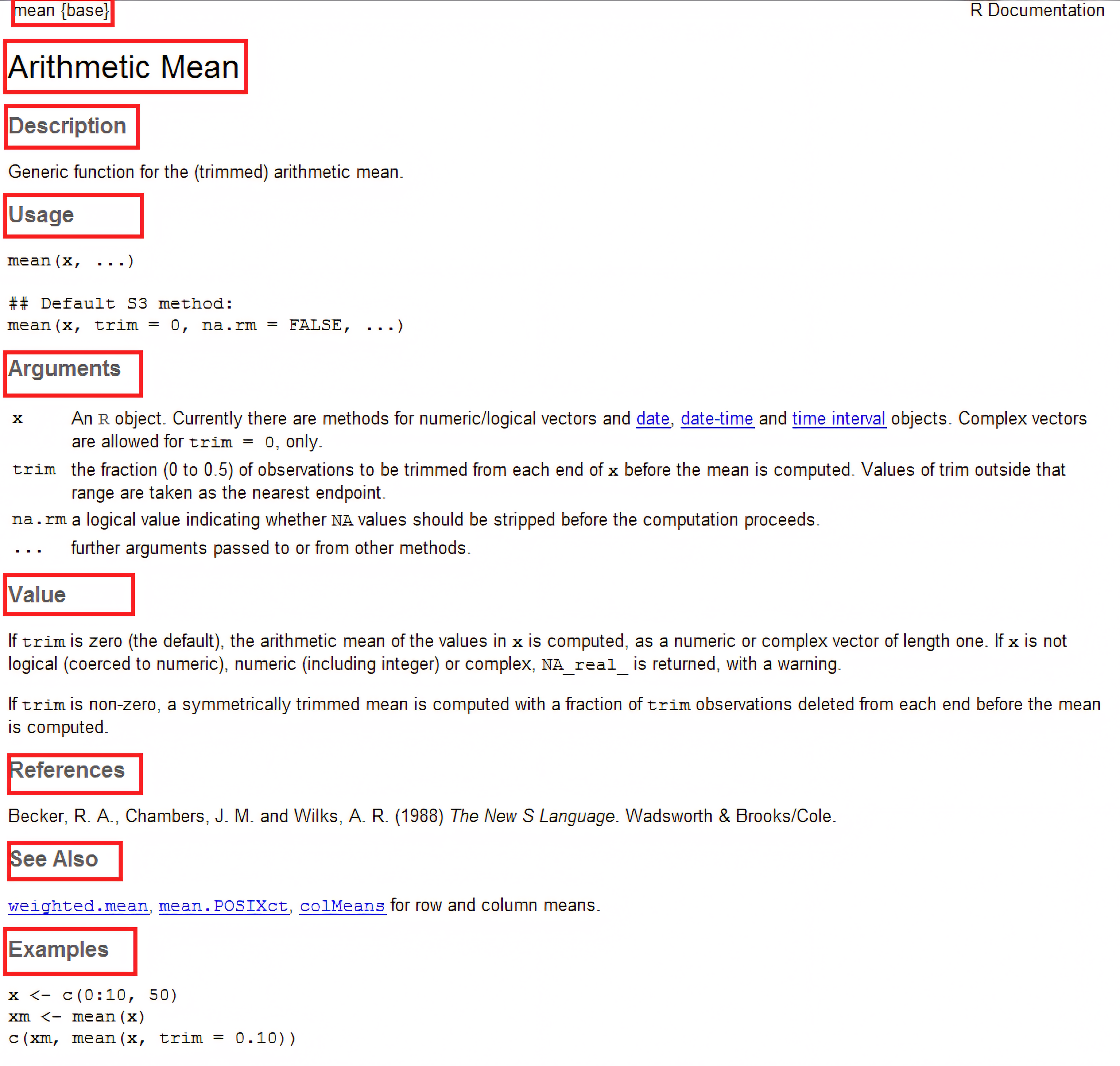
Description: descrição da função
Usage: uso da função e argumentos
Arguments: argumentos e suas especificações
Details: detalhes da função
Value: interpretar a saída (output)
Note: notas sobre a função
Authors: autores da função
References: referências bibliográficas da função
See also: funções relacionadas
Examples: exemplos do uso da função

Pacotes

Conjunto de funções extras para executar tarefas específicas

Pacotes

Duas fontes

• CRAN (Comprehensive R Archive Network)
• GitHub (Repositório de códigos)

# numero de pacotes no cran
nrow(available.packages())

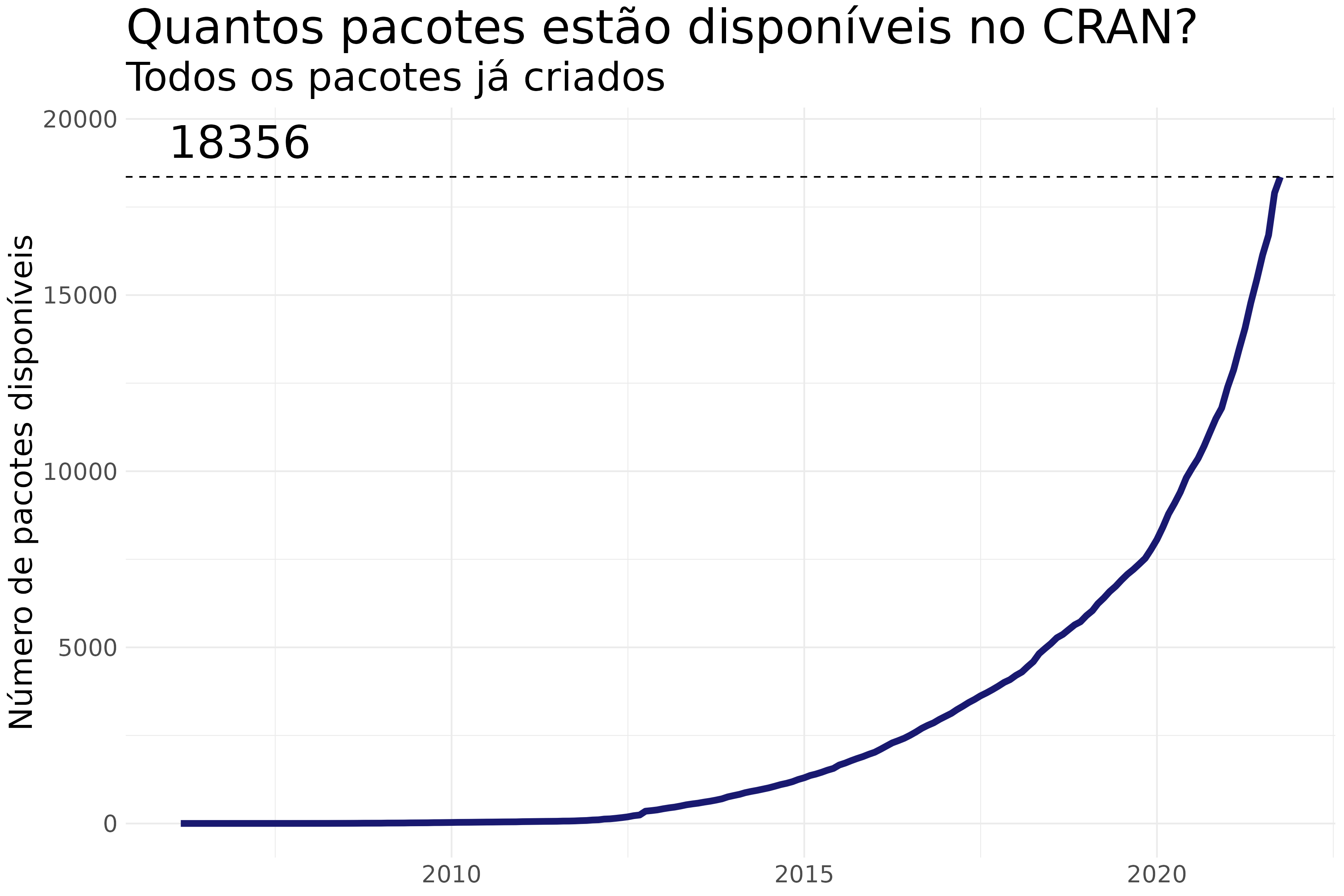
Pacotes

Instalação de pacotes

1. Download do pacote para o computador (como instalar um software/APP)
2. Precisa estar conectado à internet
3. O nome do pacote precisa estar entre aspas
4. Função (CRAN): install.packages("pacote")

Instalar o pacote vegan

# instalar pacotes
install.packages("vegan")

Verificar pacotes instalados

# verificar pacotes instalados
library()

Pacotes

Carregamento de pacotes

1. Carregar o pacote para o R (como abrir software/APP)
2. Carrega-se toda vez que se abre o R
3. Não precisa estar conectado à internet
4. O nome do pacote não precisa estar entre aspas
5. Funções: library(pacote) ou require(pacote)

Carregar o pacote vegan

# carregar pacotes
library(vegan)

Verificar pacotes carregados

# verificar pacotes carregados
search()

 [1] ".GlobalEnv"        "package:vegan"     "package:lattice"  
 [4] "package:permute"   "package:stats"     "package:graphics" 
 [7] "package:grDevices" "package:utils"     "package:datasets" 
[10] "package:methods"   "Autoloads"         "package:base"     

Principais erros

Se seu script rodou sem erros, tem algo errado…

Help me help you: um bestiário para entender erros e pedir ajuda no R

Principais erros

1. Esquecer de completar um código (+)

Parênteses

sum(1, 2
    +

Error: <text>:3:0: unexpected end of input
1: sum(1, 2
2:     +
  ^

    Aspas
    
    ::: {.cell}
    
    ```{.r .cell-code}
    "string
    +
    ```
    
    ::: {.cell-output .cell-output-error}
    ```
    Error: <text>:1:1: unexpected INCOMPLETE_STRING
    1: "string
    2: +
       ^
    ```
    :::
    :::

Principais erros

2. Esquecer da vírgula

sum(1 2)

Error: <text>:1:7: unexpected numeric constant
1: sum(1 2
          ^

3. Chamar um objeto errado

obj <- 10
OBJ

Error in eval(expr, envir, enclos): object 'OBJ' not found

Principais erros

4. Esquecer de carregar um pacote

# carregar dados
data(dune)

# funcao do pacote vegan
decostand(dune, "hell")

Error in decostand(dune, "hell"): could not find function "decostand"

Principais erros

4. Esquecer de carregar um pacote

# carregar o pacote
library(vegan)

## carregar dados
data(dune)

## funcao do pacote vegan
decostand(dune, "hell")

    Achimill  Agrostol  Airaprae  Alopgeni  Anthodor  Bellpere  Bromhord
1  0.2357023 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
2  0.2672612 0.0000000 0.0000000 0.2182179 0.0000000 0.2672612 0.3086067
3  0.0000000 0.3162278 0.0000000 0.4183300 0.0000000 0.2236068 0.0000000
4  0.0000000 0.4216370 0.0000000 0.2108185 0.0000000 0.2108185 0.2581989
5  0.2156655 0.0000000 0.0000000 0.0000000 0.3049971 0.2156655 0.2156655
6  0.2041241 0.0000000 0.0000000 0.0000000 0.2500000 0.0000000 0.0000000
7  0.2236068 0.0000000 0.0000000 0.0000000 0.2236068 0.0000000 0.2236068
8  0.0000000 0.3162278 0.0000000 0.3535534 0.0000000 0.0000000 0.0000000
9  0.0000000 0.2672612 0.0000000 0.2672612 0.0000000 0.0000000 0.0000000
10 0.3049971 0.0000000 0.0000000 0.0000000 0.3049971 0.2156655 0.3049971
11 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
12 0.0000000 0.3380617 0.0000000 0.4780914 0.0000000 0.0000000 0.0000000
13 0.0000000 0.3892495 0.0000000 0.3892495 0.0000000 0.0000000 0.0000000
14 0.0000000 0.4082483 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
15 0.0000000 0.4170288 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
16 0.0000000 0.4605662 0.0000000 0.3481553 0.0000000 0.0000000 0.0000000
17 0.3651484 0.0000000 0.3651484 0.0000000 0.5163978 0.0000000 0.0000000
18 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.2721655 0.0000000
19 0.0000000 0.0000000 0.3110855 0.0000000 0.3592106 0.0000000 0.0000000
20 0.0000000 0.4016097 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
    Chenalbu  Cirsarve  Comapalu  Eleopalu  Elymrepe  Empenigr  Hyporadi
1  0.0000000 0.0000000 0.0000000 0.0000000 0.4714045 0.0000000 0.0000000
2  0.0000000 0.0000000 0.0000000 0.0000000 0.3086067 0.0000000 0.0000000
3  0.0000000 0.0000000 0.0000000 0.0000000 0.3162278 0.0000000 0.0000000
4  0.0000000 0.2108185 0.0000000 0.0000000 0.2981424 0.0000000 0.0000000
5  0.0000000 0.0000000 0.0000000 0.0000000 0.3049971 0.0000000 0.0000000
6  0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
7  0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
8  0.0000000 0.0000000 0.0000000 0.3162278 0.0000000 0.0000000 0.0000000
9  0.0000000 0.0000000 0.0000000 0.0000000 0.3779645 0.0000000 0.0000000
10 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
11 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.2500000
12 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
13 0.1740777 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
14 0.0000000 0.0000000 0.2886751 0.4082483 0.0000000 0.0000000 0.0000000
15 0.0000000 0.0000000 0.2948839 0.4662524 0.0000000 0.0000000 0.0000000
16 0.0000000 0.0000000 0.0000000 0.4923660 0.0000000 0.0000000 0.0000000
17 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.3651484
18 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
19 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.2540003 0.4016097
20 0.0000000 0.0000000 0.0000000 0.3592106 0.0000000 0.0000000 0.0000000
    Juncarti  Juncbufo  Lolipere  Planlanc   Poaprat   Poatriv  Ranuflam
1  0.0000000 0.0000000 0.6236096 0.0000000 0.4714045 0.3333333 0.0000000
2  0.0000000 0.0000000 0.3450328 0.0000000 0.3086067 0.4082483 0.0000000
3  0.0000000 0.0000000 0.3872983 0.0000000 0.3535534 0.3872983 0.0000000
4  0.0000000 0.0000000 0.3333333 0.0000000 0.2981424 0.3333333 0.0000000
5  0.0000000 0.0000000 0.2156655 0.3409972 0.2156655 0.3735437 0.0000000
6  0.0000000 0.0000000 0.3535534 0.3227486 0.2500000 0.2886751 0.0000000
7  0.0000000 0.2236068 0.3872983 0.3535534 0.3162278 0.3535534 0.0000000
8  0.3162278 0.0000000 0.3162278 0.0000000 0.3162278 0.3162278 0.2236068
9  0.3086067 0.3086067 0.2182179 0.0000000 0.3086067 0.3450328 0.0000000
10 0.0000000 0.0000000 0.3735437 0.2641353 0.3049971 0.3049971 0.0000000
11 0.0000000 0.0000000 0.4677072 0.3061862 0.3535534 0.0000000 0.0000000
12 0.0000000 0.3380617 0.0000000 0.0000000 0.0000000 0.3380617 0.0000000
13 0.0000000 0.3015113 0.0000000 0.0000000 0.2461830 0.5222330 0.2461830
14 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.2886751
15 0.3611576 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.2948839
16 0.3015113 0.0000000 0.0000000 0.0000000 0.0000000 0.2461830 0.2461830
17 0.0000000 0.0000000 0.0000000 0.3651484 0.2581989 0.0000000 0.0000000
18 0.0000000 0.0000000 0.2721655 0.3333333 0.3333333 0.0000000 0.0000000
19 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
20 0.3592106 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.3592106
    Rumeacet  Sagiproc  Salirepe  Scorautu  Trifprat  Trifrepe  Vicilath
1  0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
2  0.0000000 0.0000000 0.0000000 0.3450328 0.0000000 0.3450328 0.0000000
3  0.0000000 0.0000000 0.0000000 0.2236068 0.0000000 0.2236068 0.0000000
4  0.0000000 0.3333333 0.0000000 0.2108185 0.0000000 0.1490712 0.0000000
5  0.3409972 0.0000000 0.0000000 0.2641353 0.2156655 0.2156655 0.0000000
6  0.3535534 0.0000000 0.0000000 0.2500000 0.3227486 0.3227486 0.0000000
7  0.2738613 0.0000000 0.0000000 0.2738613 0.2236068 0.2236068 0.0000000
8  0.0000000 0.2236068 0.0000000 0.2738613 0.0000000 0.2236068 0.0000000
9  0.2182179 0.2182179 0.0000000 0.2182179 0.0000000 0.2672612 0.0000000
10 0.0000000 0.0000000 0.0000000 0.2641353 0.0000000 0.3735437 0.1524986
11 0.0000000 0.2500000 0.0000000 0.3952847 0.0000000 0.3061862 0.2500000
12 0.2390457 0.3380617 0.0000000 0.2390457 0.0000000 0.2927700 0.0000000
13 0.0000000 0.2461830 0.0000000 0.2461830 0.0000000 0.2461830 0.0000000
14 0.0000000 0.0000000 0.0000000 0.2886751 0.0000000 0.5000000 0.0000000
15 0.0000000 0.0000000 0.0000000 0.2948839 0.0000000 0.2085144 0.0000000
16 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
17 0.0000000 0.0000000 0.0000000 0.3651484 0.0000000 0.0000000 0.0000000
18 0.0000000 0.0000000 0.3333333 0.4303315 0.0000000 0.2721655 0.1924501
19 0.0000000 0.3110855 0.3110855 0.4399413 0.0000000 0.2540003 0.0000000
20 0.0000000 0.0000000 0.4016097 0.2540003 0.0000000 0.0000000 0.0000000
    Bracruta  Callcusp
1  0.0000000 0.0000000
2  0.0000000 0.0000000
3  0.2236068 0.0000000
4  0.2108185 0.0000000
5  0.2156655 0.0000000
6  0.3535534 0.0000000
7  0.2236068 0.0000000
8  0.2236068 0.0000000
9  0.2182179 0.0000000
10 0.2156655 0.0000000
11 0.3535534 0.0000000
12 0.3380617 0.0000000
13 0.0000000 0.0000000
14 0.0000000 0.4082483
15 0.4170288 0.0000000
16 0.3481553 0.3015113
17 0.0000000 0.0000000
18 0.4714045 0.0000000
19 0.3110855 0.0000000
20 0.3592106 0.3110855

Principais erros

5. Usar o nome da função de forma errônea

colsums(dune)

Error in colsums(dune): could not find function "colsums"

colSums(dune)

Achimill Agrostol Airaprae Alopgeni Anthodor Bellpere Bromhord Chenalbu 
      16       48        5       36       21       13       15        1 
Cirsarve Comapalu Eleopalu Elymrepe Empenigr Hyporadi Juncarti Juncbufo 
       2        4       25       26        2        9       18       13 
Lolipere Planlanc  Poaprat  Poatriv Ranuflam Rumeacet Sagiproc Salirepe 
      58       26       48       63       14       18       20       11 
Scorautu Trifprat Trifrepe Vicilath Bracruta Callcusp 
      54        9       47        4       49       10 

Dúvidas?

2. Análise exploratória de dados (AED)

Dados

id	especie	peso	comp_corpo	comp_asa	…
LECAVE035	Columbina talpacoti	40.64	158.5	90.51	…
LECAVE036	Columbina talpacoti	41.05	149.73	89.42	…
LECAVE037	Columbina talpacoti	43.96	147.62	89.32	…
LECAVE038	Columbina talpacoti	48.01	153.44	90.57	…
…	…	…	…	…	…

Variáveis

Cada coluna dos nossos dados é uma variável (valores variam)

Rows: 16
Columns: 8
$ id         <chr> "LECAVE040", "LECAVE041", "LECAVE043", "LECAVE044", "LECAVE…
$ especie    <chr> "Thraupis sayaca", "Thraupis sayaca", "Thraupis sayaca", "T…
$ peso       <dbl> 22.77, 18.22, 24.09, 17.34, 20.75, 26.90, 23.90, 26.80, 32.…
$ comp_corpo <dbl> 146.58, 139.79, 120.63, 133.33, 139.80, 140.45, 136.39, 119…
$ comp_bico  <dbl> 16.57, 17.14, 19.06, 18.49, 15.68, 9.69, 14.94, 11.13, 13.0…
$ larg_bico  <dbl> 6.96, 6.94, 6.64, 7.11, 7.13, 7.75, 6.59, 6.55, 6.77, 8.40,…
$ alt_bico   <dbl> 6.60, 8.51, 8.23, 6.97, 7.12, 5.92, 7.12, 7.30, 7.35, 7.95,…
$ sexo       <chr> "F", "F", "F", "F", "F", "M", "F", "M", "M", "F", "M", "M",…

Medidas-resumo

Medidas de posição

• Moda: valor mais frequente das observações

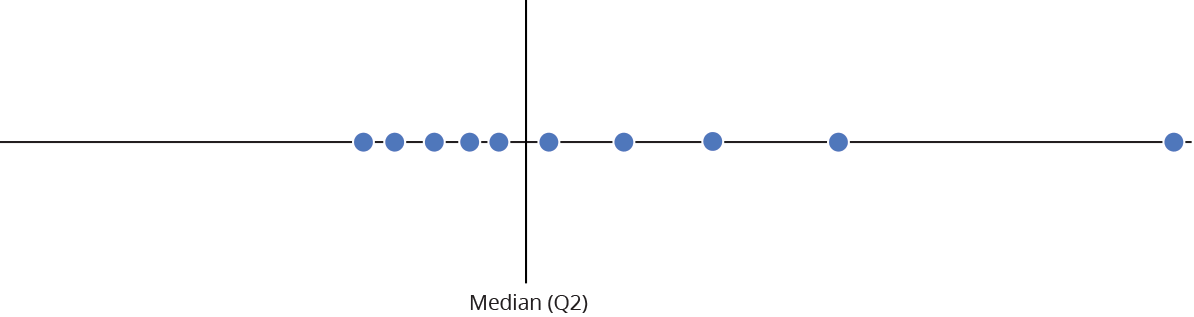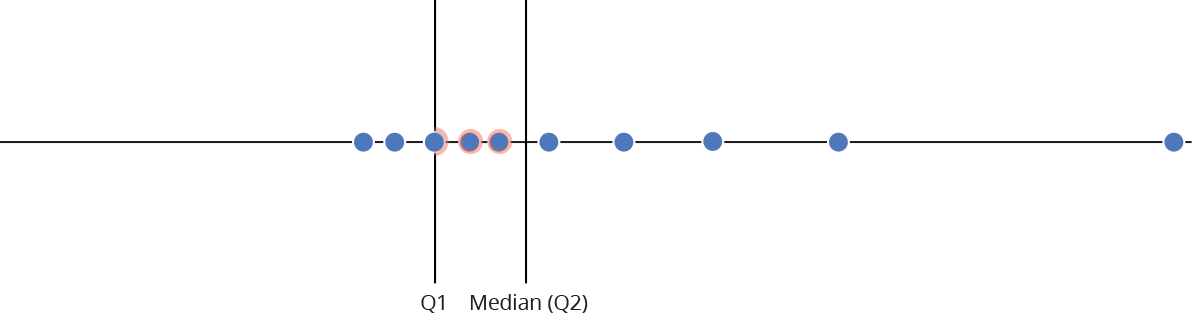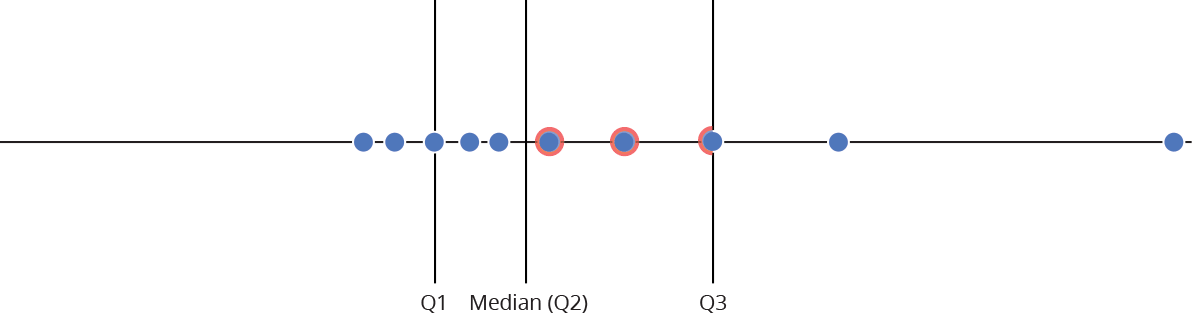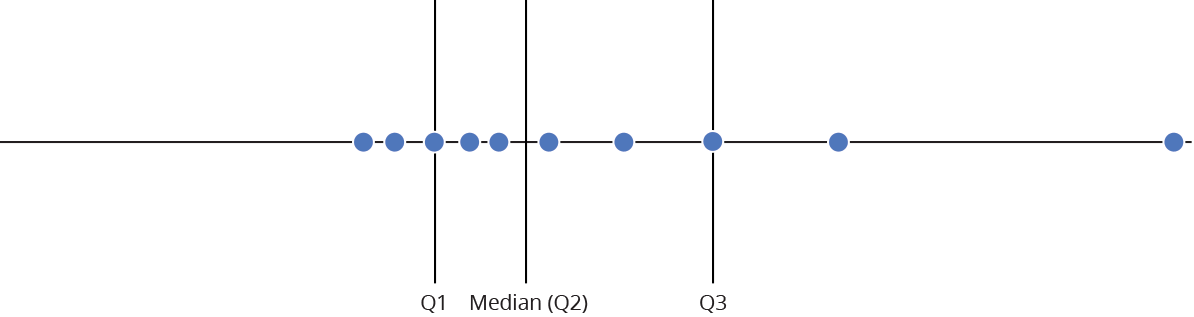
• Mediana: valor que divide as observações ordenadas em duas partes iguais

• Média aritmética: soma das observações dividida pelo número de observações

• Outras médias: ponderada, geométrica e harmônica

Medidas-resumo

Medidas de dispersão

• Variância: medida de quantas observações diferem do valor central (média)

• Desvio padrão: raiz quadrada da variância (mantêm a mesma unidade de medida)

• Erro padrão: variação da média amostral em relação à média populacional (confiabilidade da média amostral)

Tabelas

Tabelas de frequência

• Dados brutos: conjunto dos valores numéricos coletados na pesquisa

• Classes: intervalo de valores contínuos (0 |— 1)

• Frequência absoluta (fi): número de vezes que uma observação aparece ou pertencente a um intervalo ou classe

• Frequência total: soma de todas as frequências absolutas (fi)

• Frequência relativa (fri): valor da razão de cada frequência absoluta (fi) com a frequência total (somatório de fi)

• Frequência acumulada (Fi): obtida somando (acumulando) os valores da frequência absoluta (fi)

• Frequência relativa acumulada (Fri): obtida somando (acumulando) os valores da frequência relativa (fri)

Tabelas

Tabelas de frequência

Classes	Freq. absoluta (fi)	Freq. relativa (fri)	Freq. acumulada (Fi)	Freq. relativa acumulada (Fri)
0|—1	4	0.13	4	0.13
1|—2	8	0.26	12	0.39
2|—3	12	0.39	24	0.77
3|—4	7	0.23	31	1.00
Total	31	1.00

Gráficos

• Melhor forma de apresentar, sintetizar, discutir e interpretar seus dados

• Necessário em quase todas as análises estatísticas

• Necessário em quase todas as publicações, trabalhos de consultoria, TCC, dissertação, tese, etc.

• Existem vários tipos de gráficos para representar os padrões em seus dados para diferentes tipos de finalidades

• De forma simplificada, os gráficos são representações dos nossos dados tabulares

Como mentir com estatística?

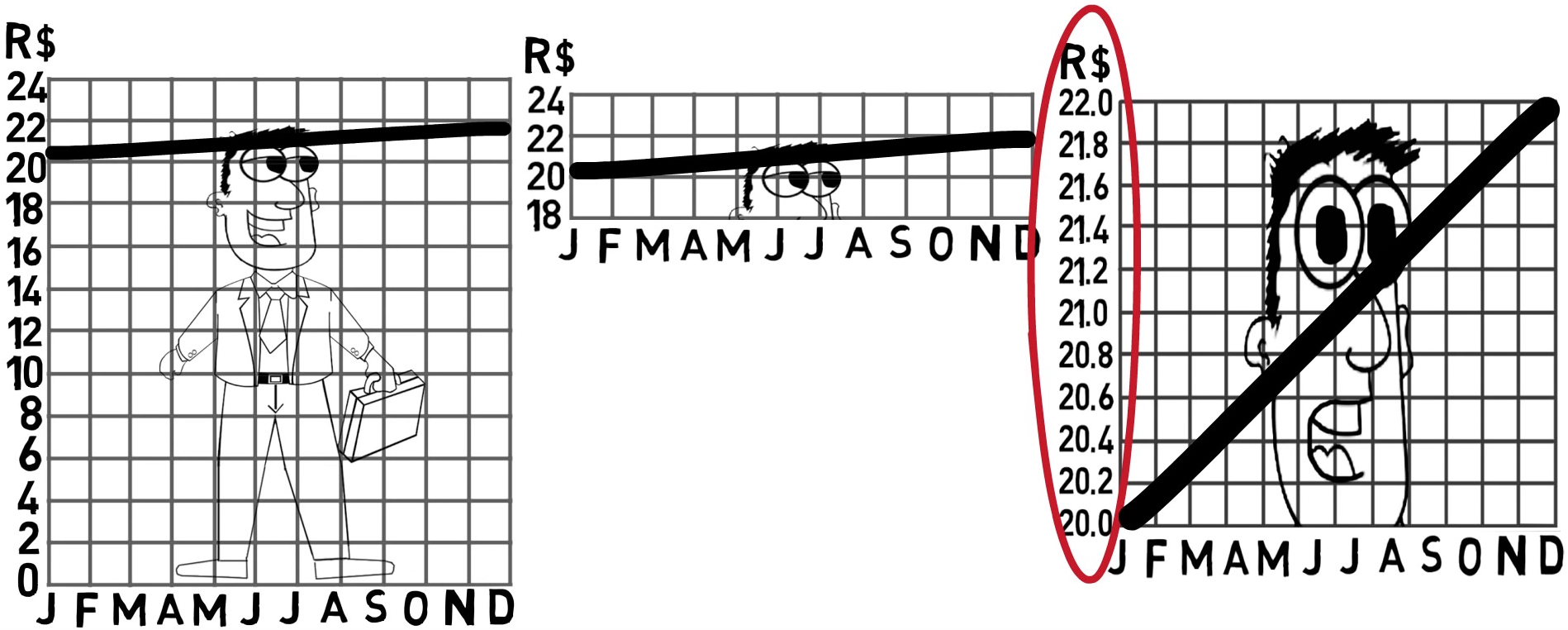
Elementos de um gráfico

Representações das colunas (eixos) e linhas (elementos)

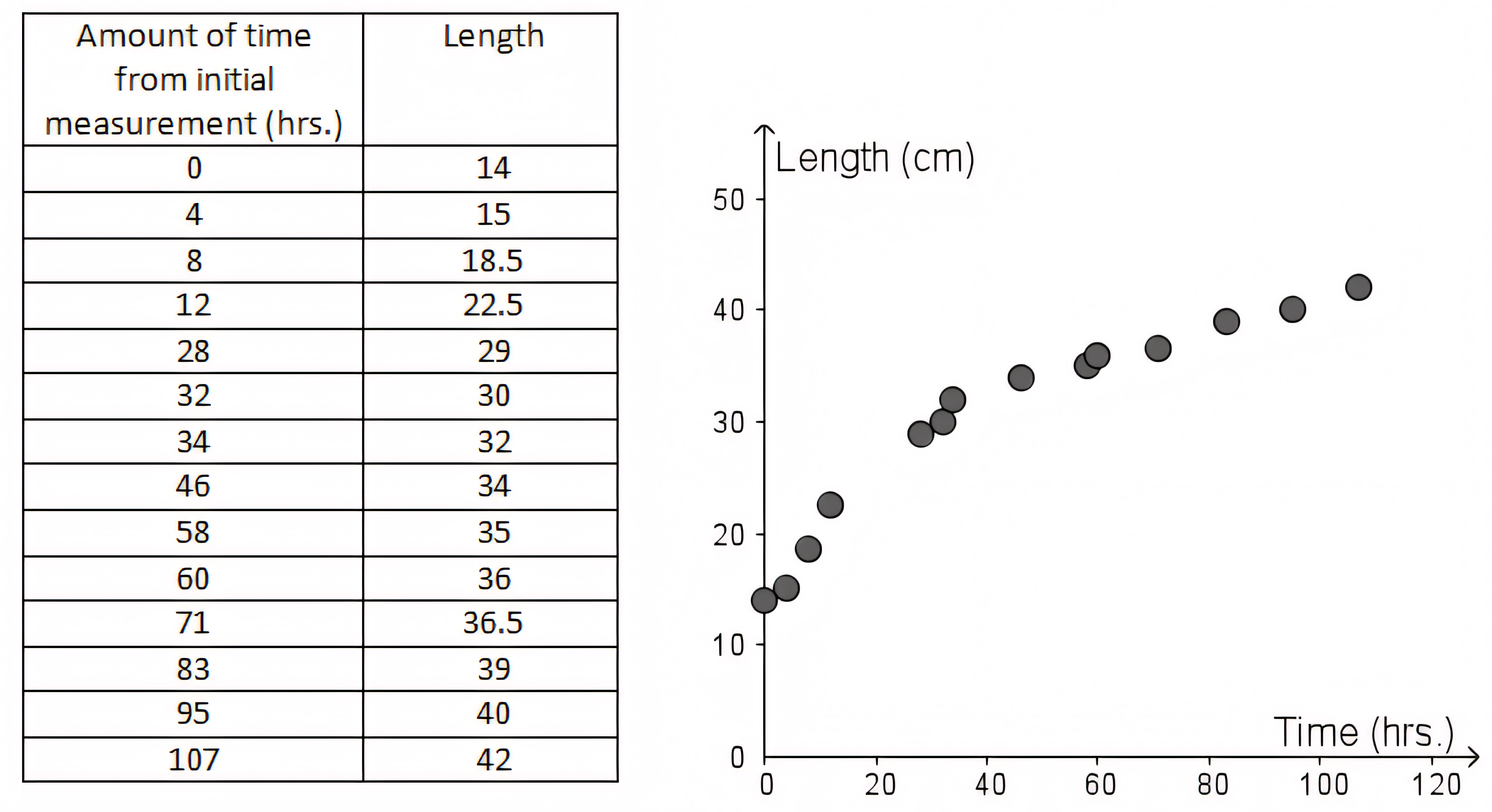
Tipos de variáveis

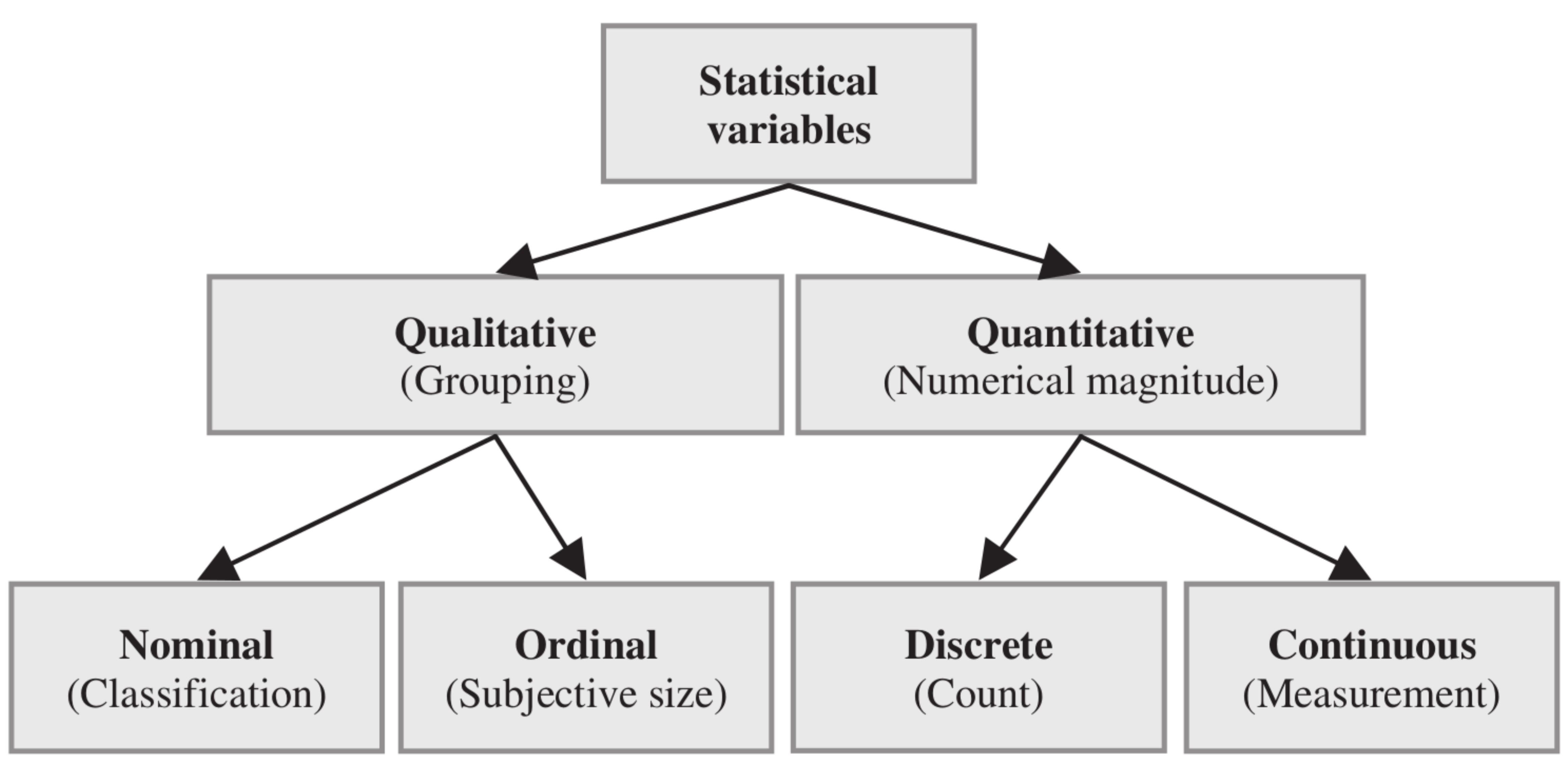
Tipos de variáveis e tipos gráficos

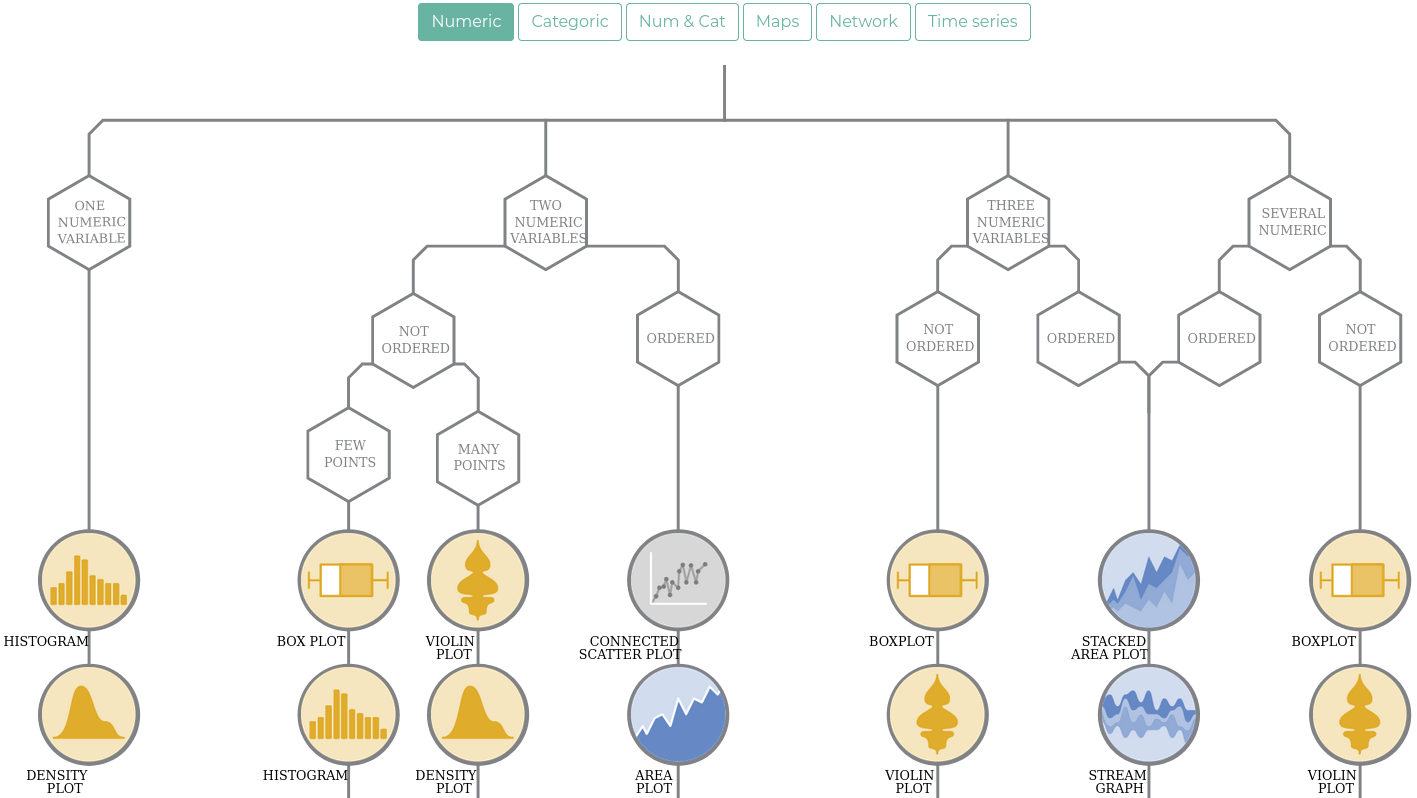
Tipos de variáveis e tipos gráficos

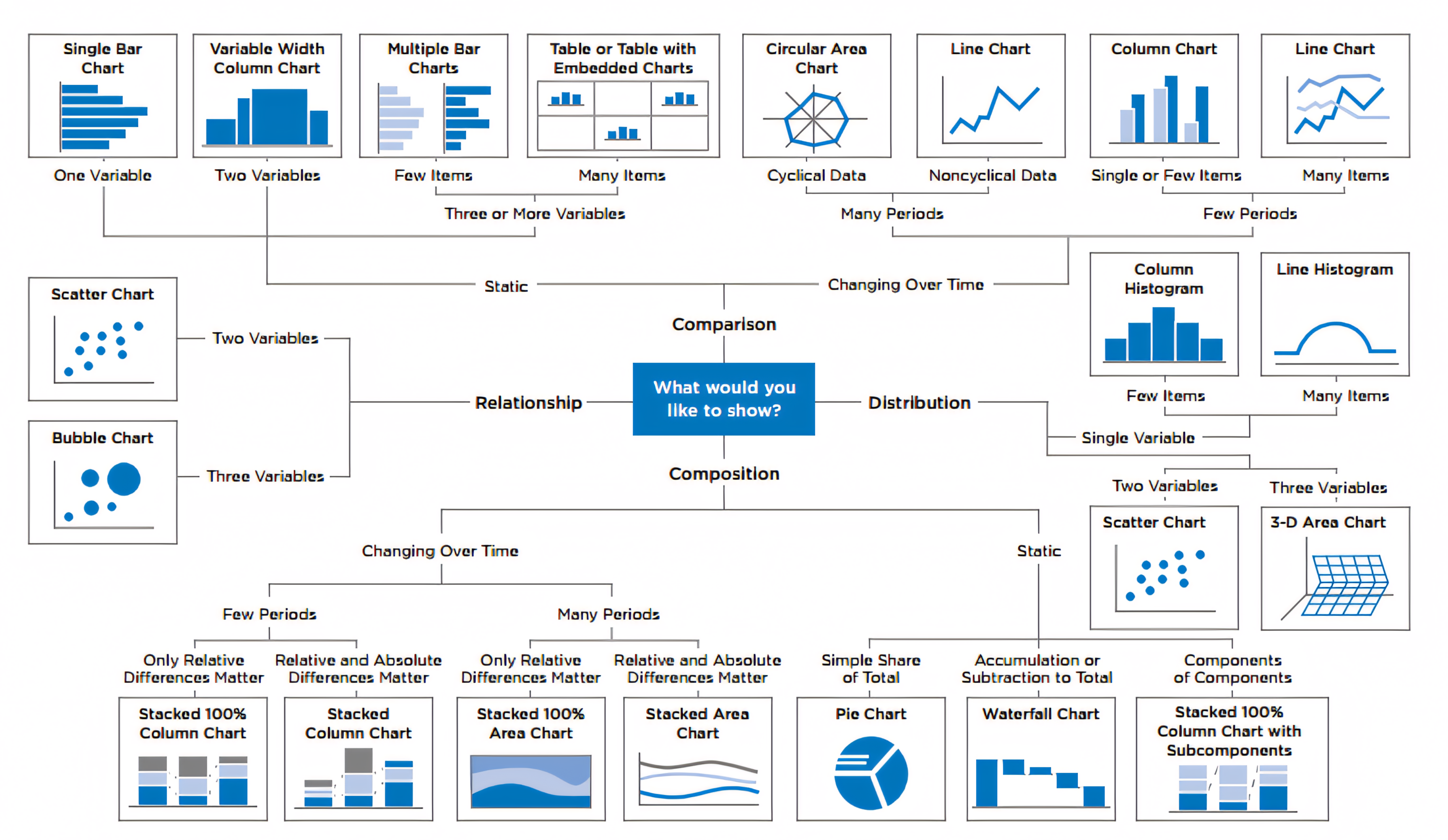
R CHARTS

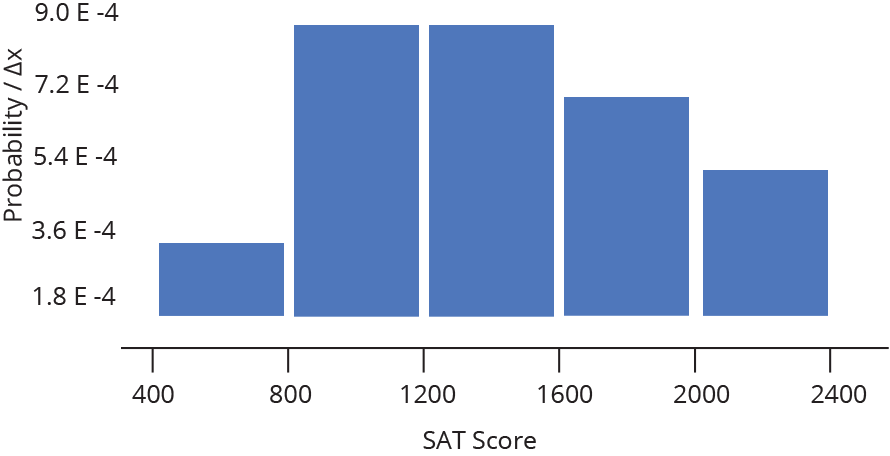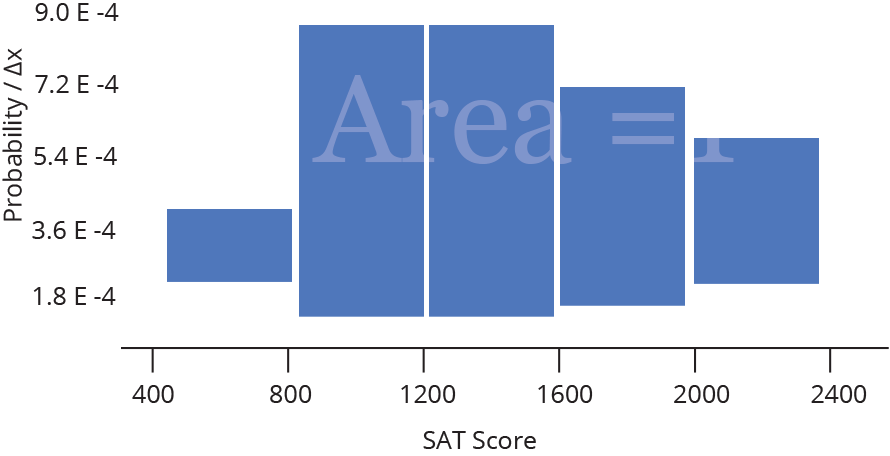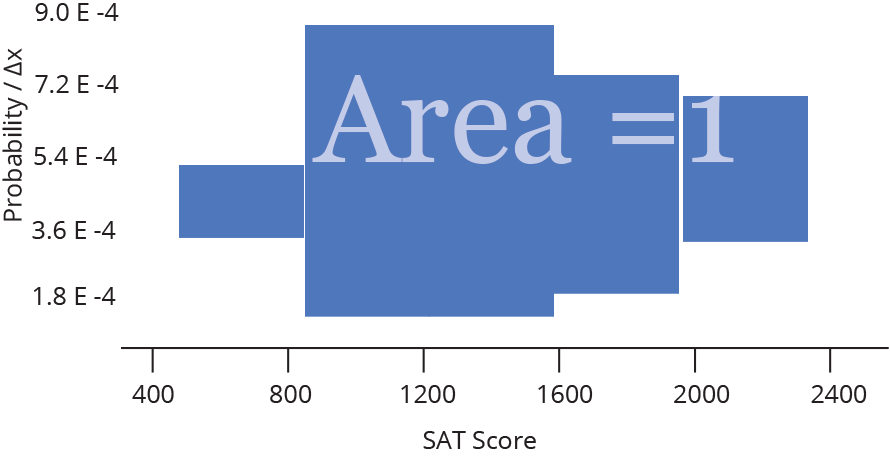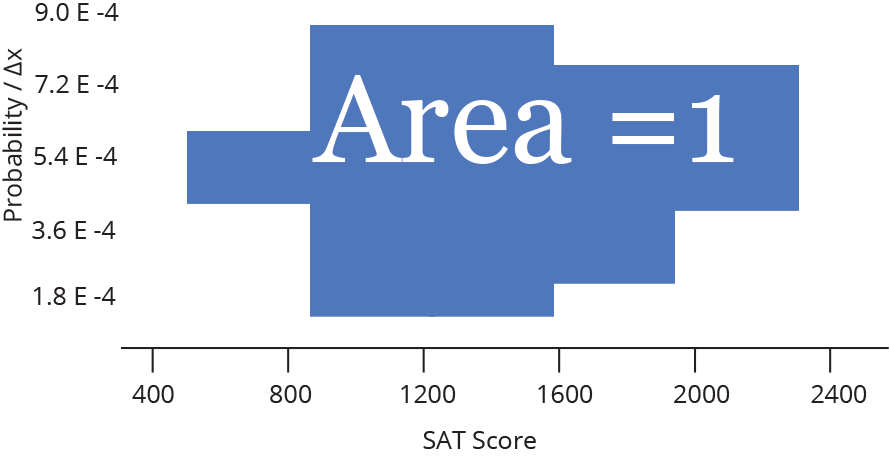
Histograma ou densidade

• Representa dados de uma coluna

• Dados do tipo discreto ou contínuo

• Distribuição de frequência ou densidade

Histograma

Histograma

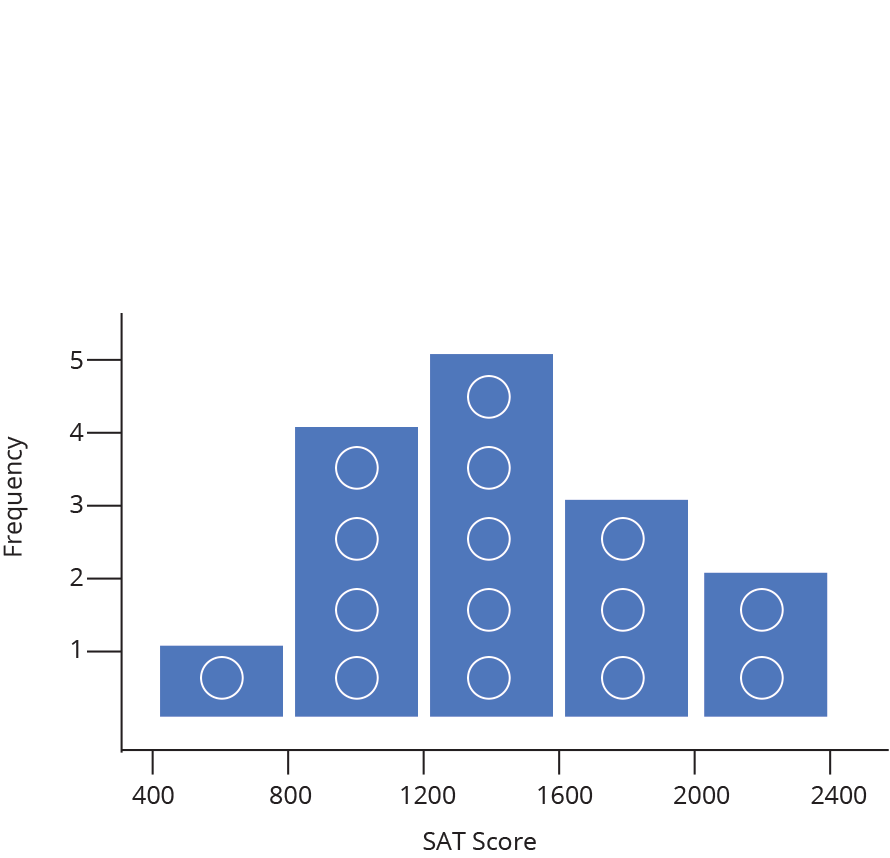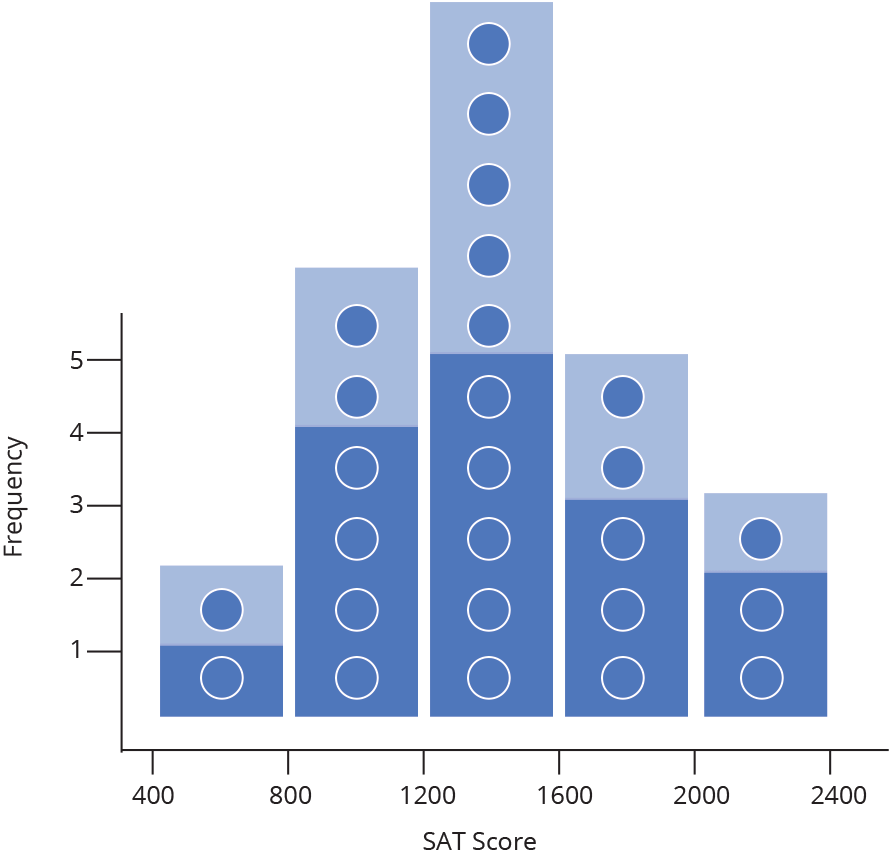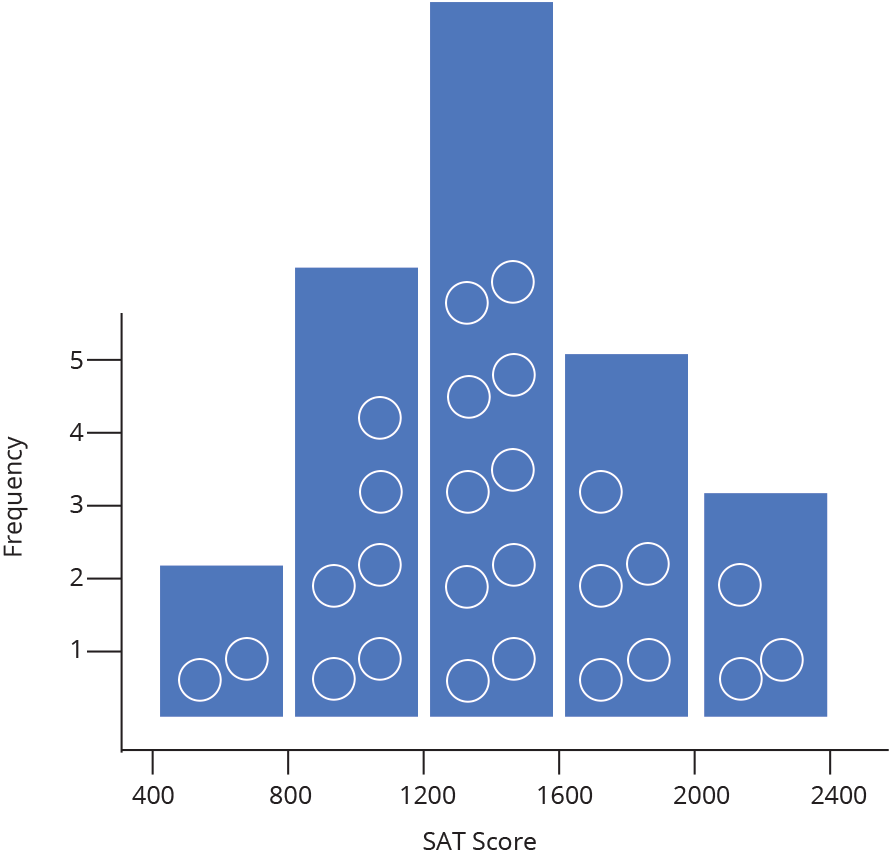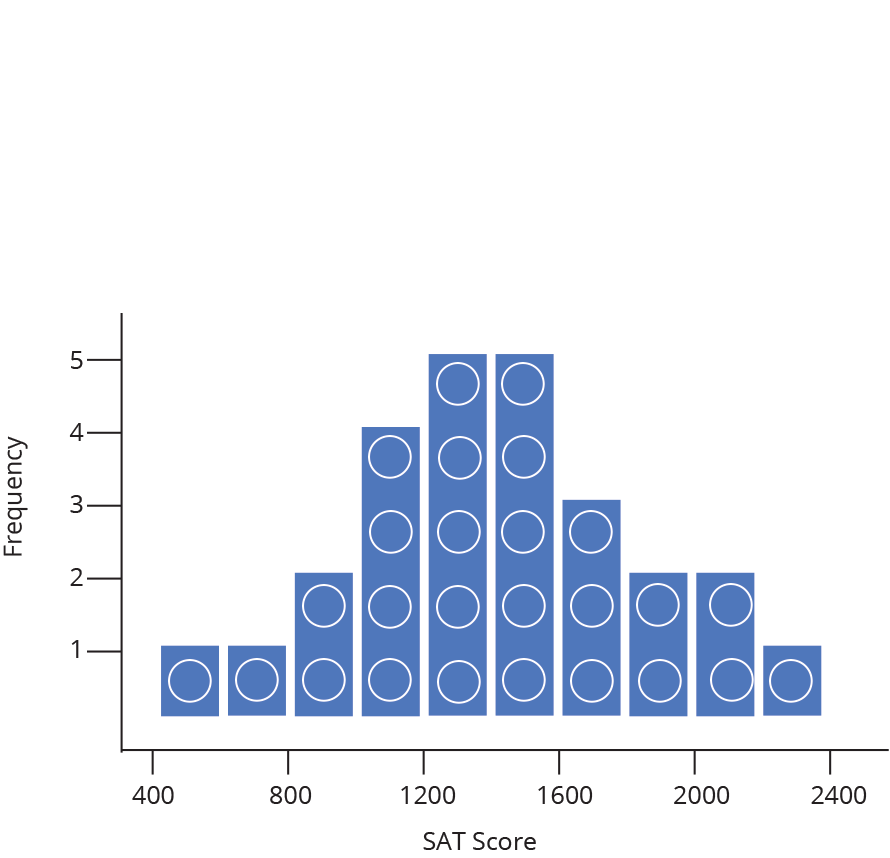
Densidade

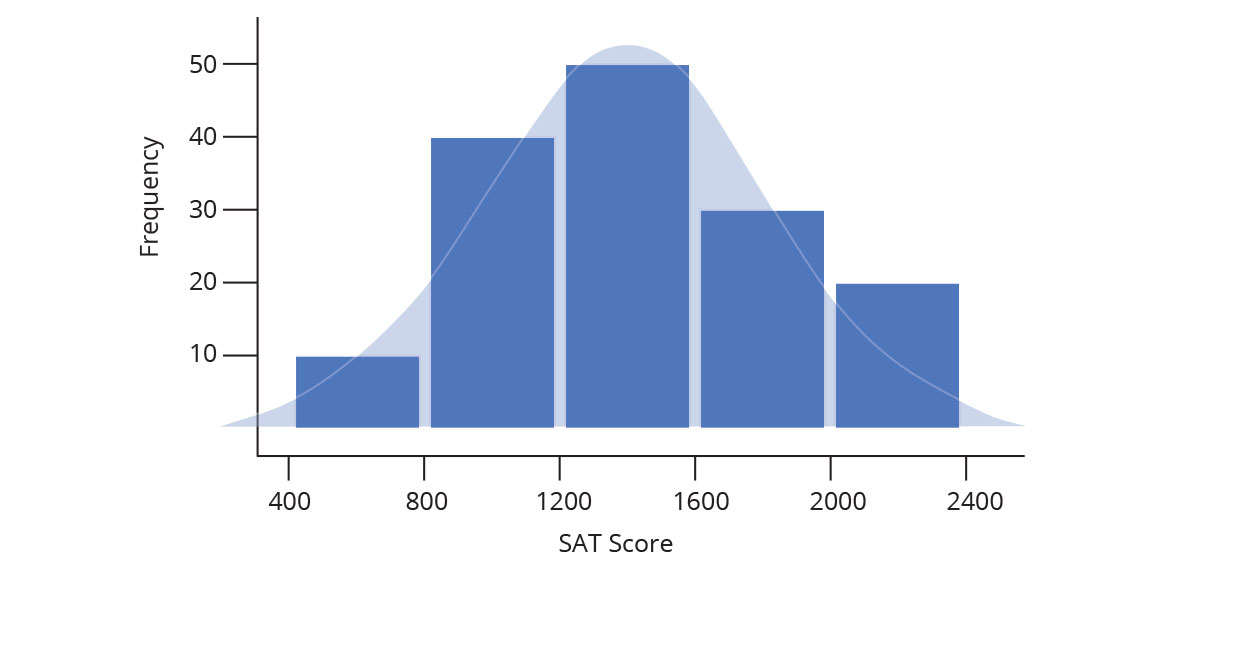
Densidade

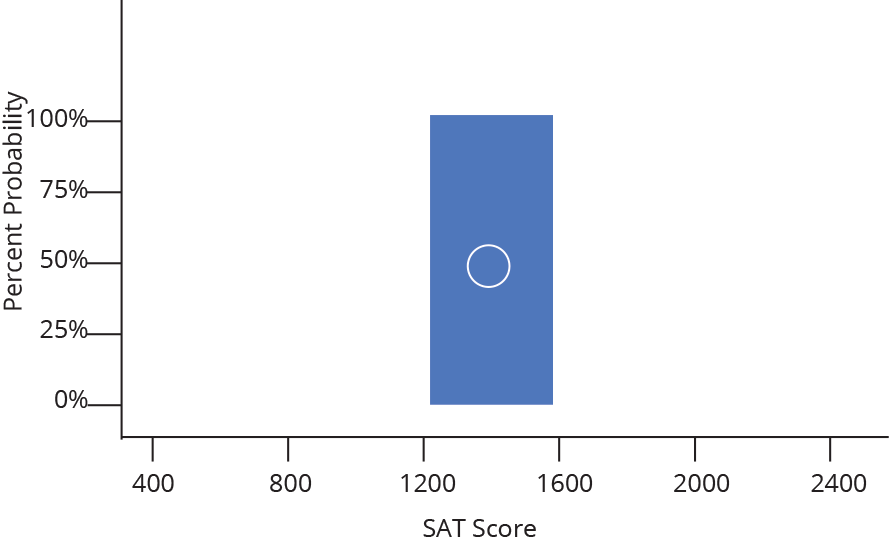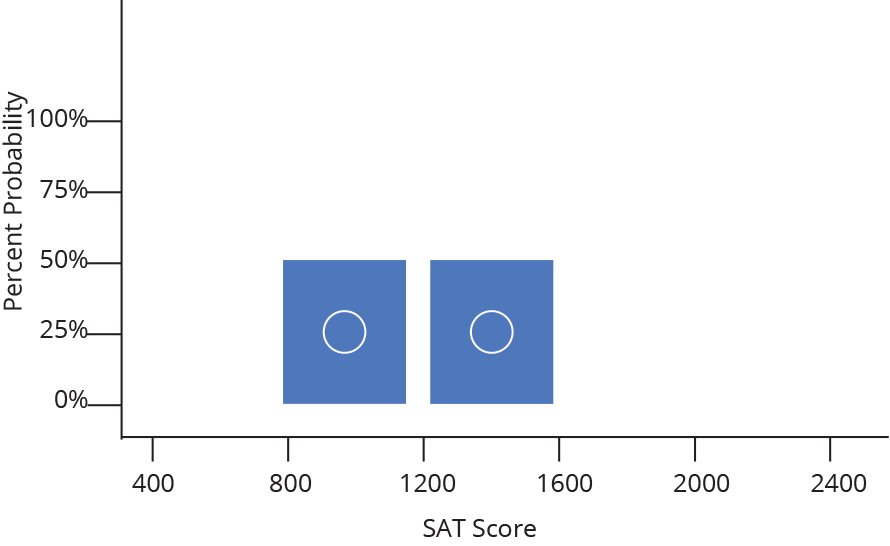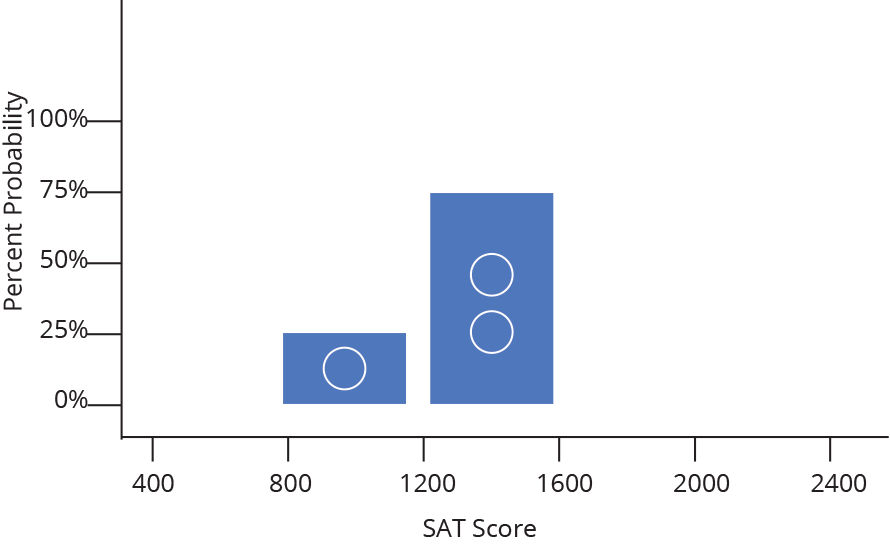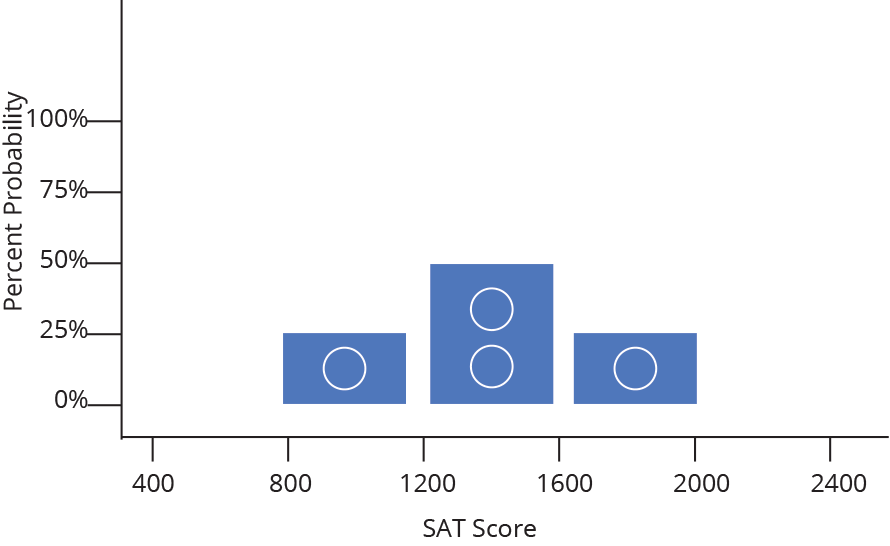
Gráfico de caixas (Box plot)

• Representa dados de duas colunas

• Dados do tipo categóricos: X = categórico e Y = contínuo

• Resume informações de medidas contínuas para dois ou mais fatores categóricos

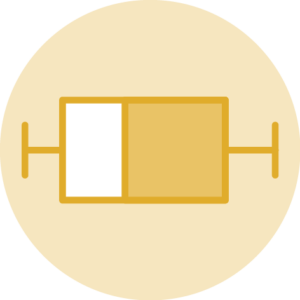
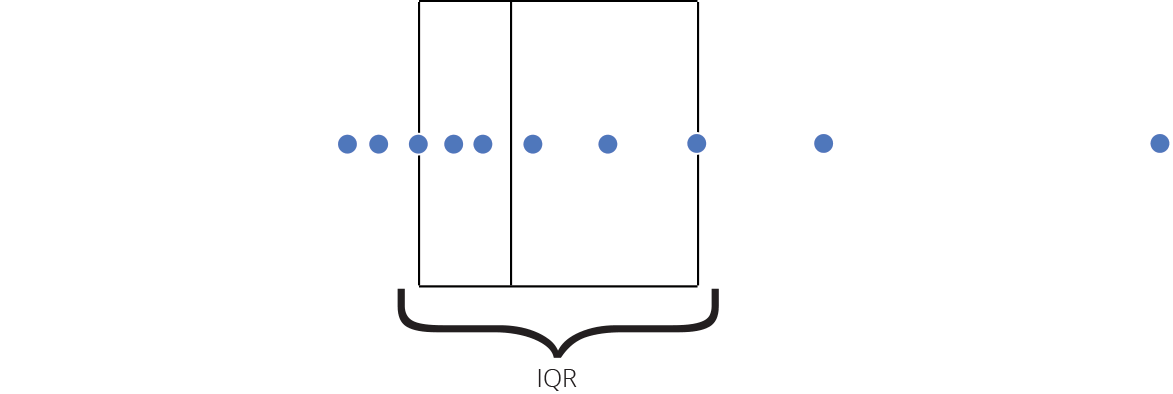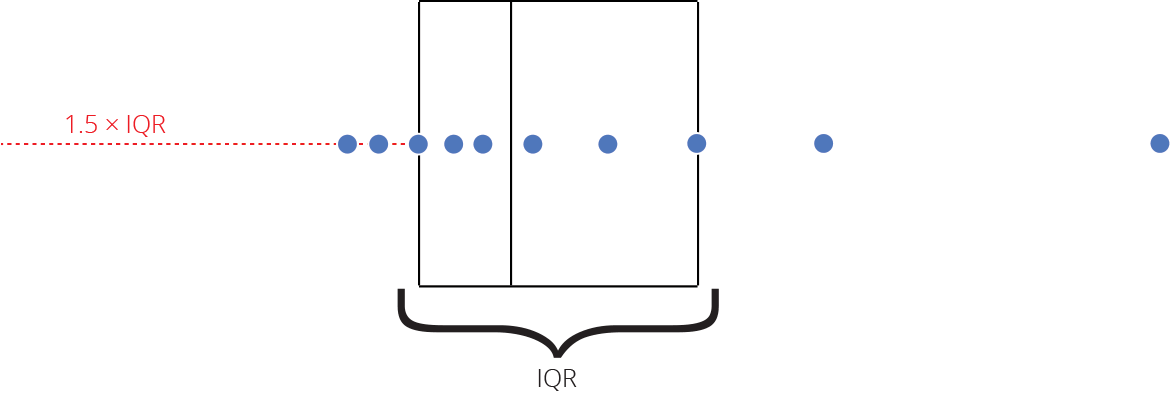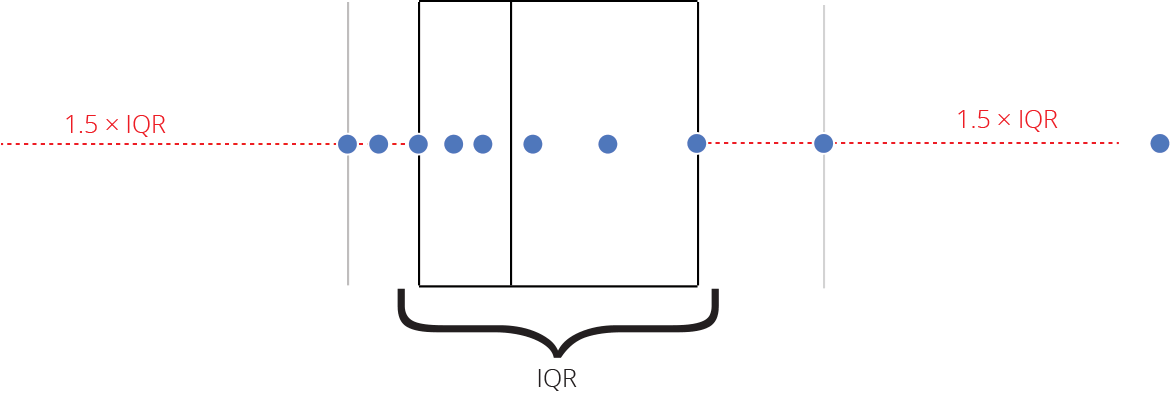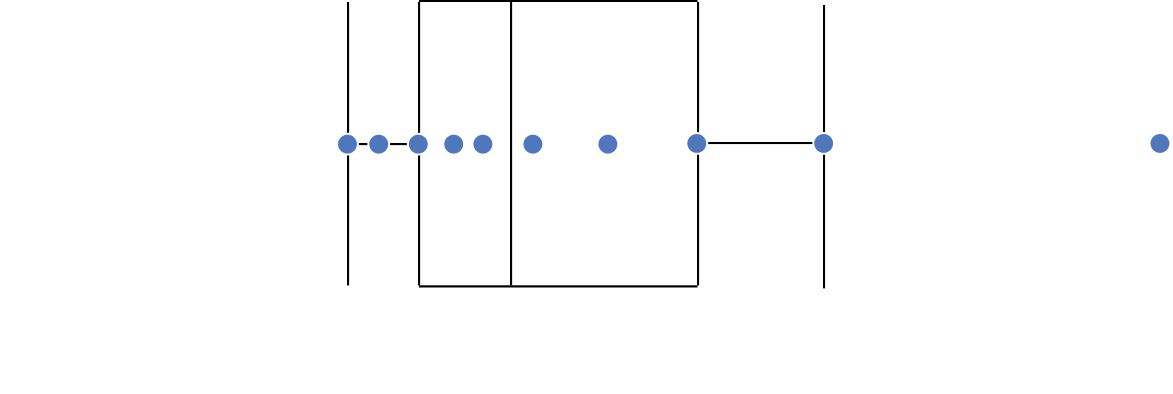
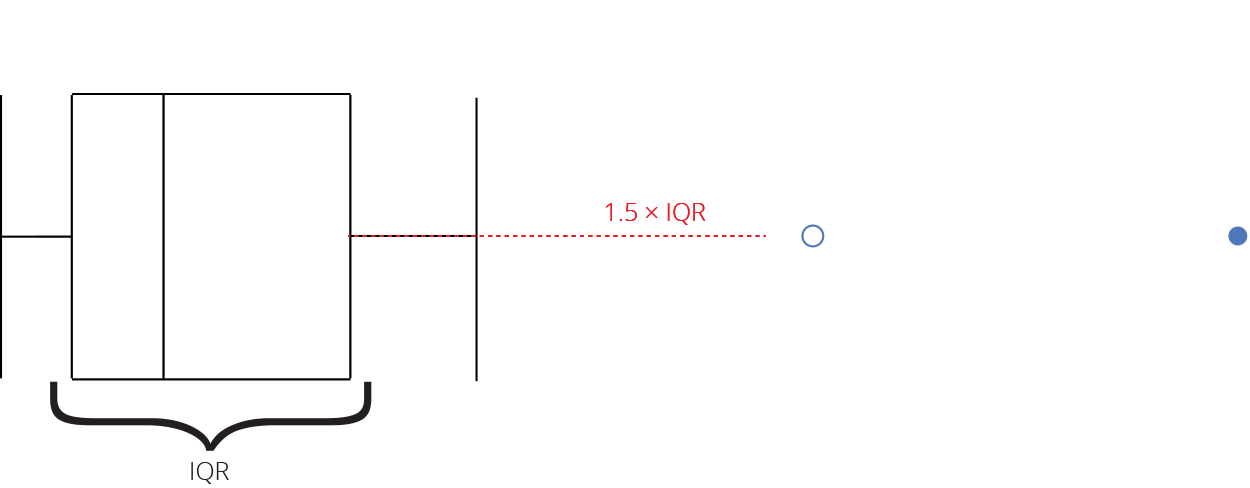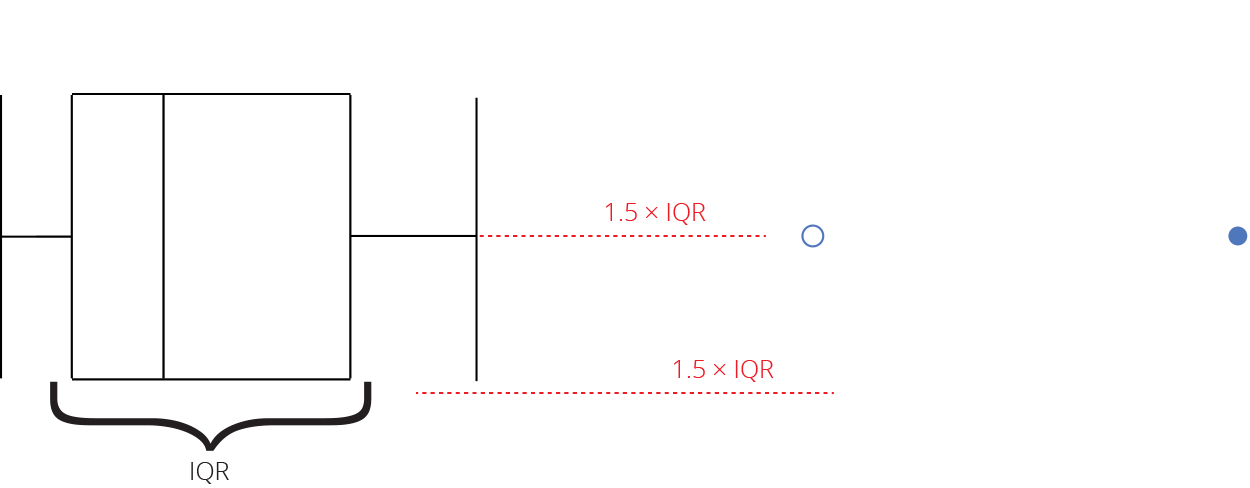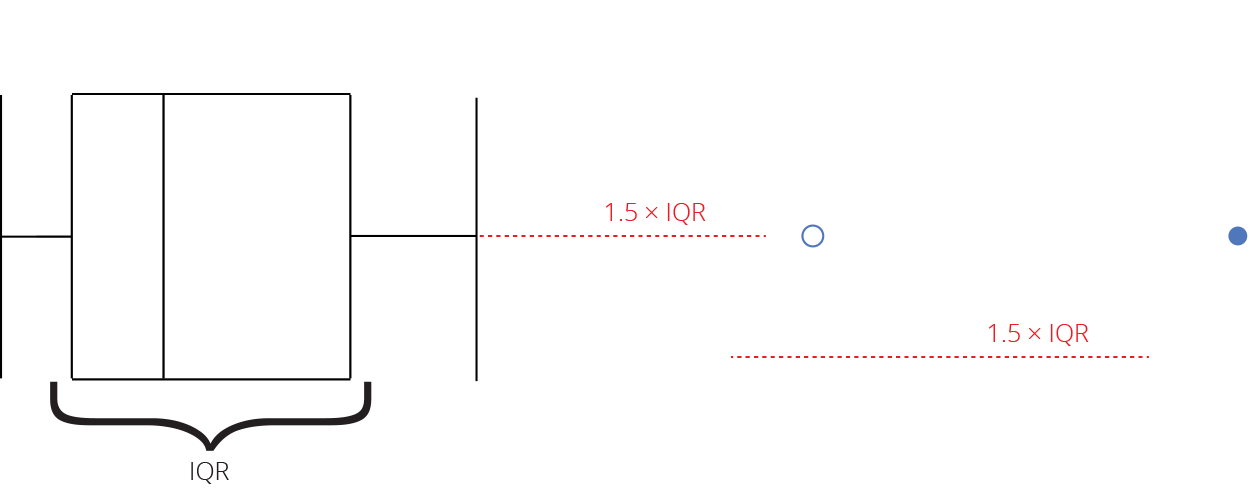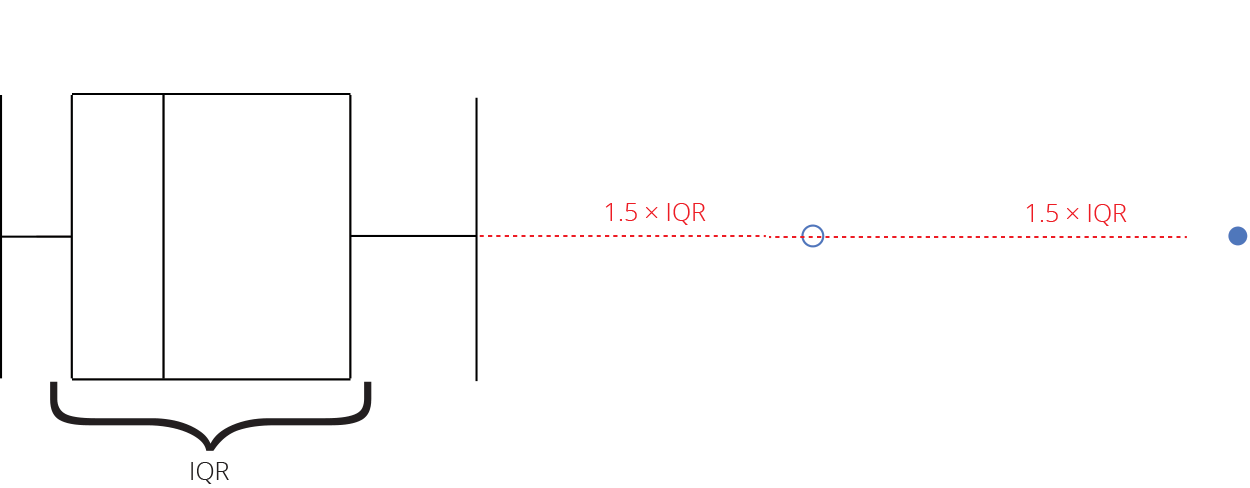
Gráfico de caixas (Box plot)

• Intervalo inter-quartil (interquartile range - IQR)

• Limite inferior e limite superipor (1.5 x IQR)

• Valores exteriores (outliers)

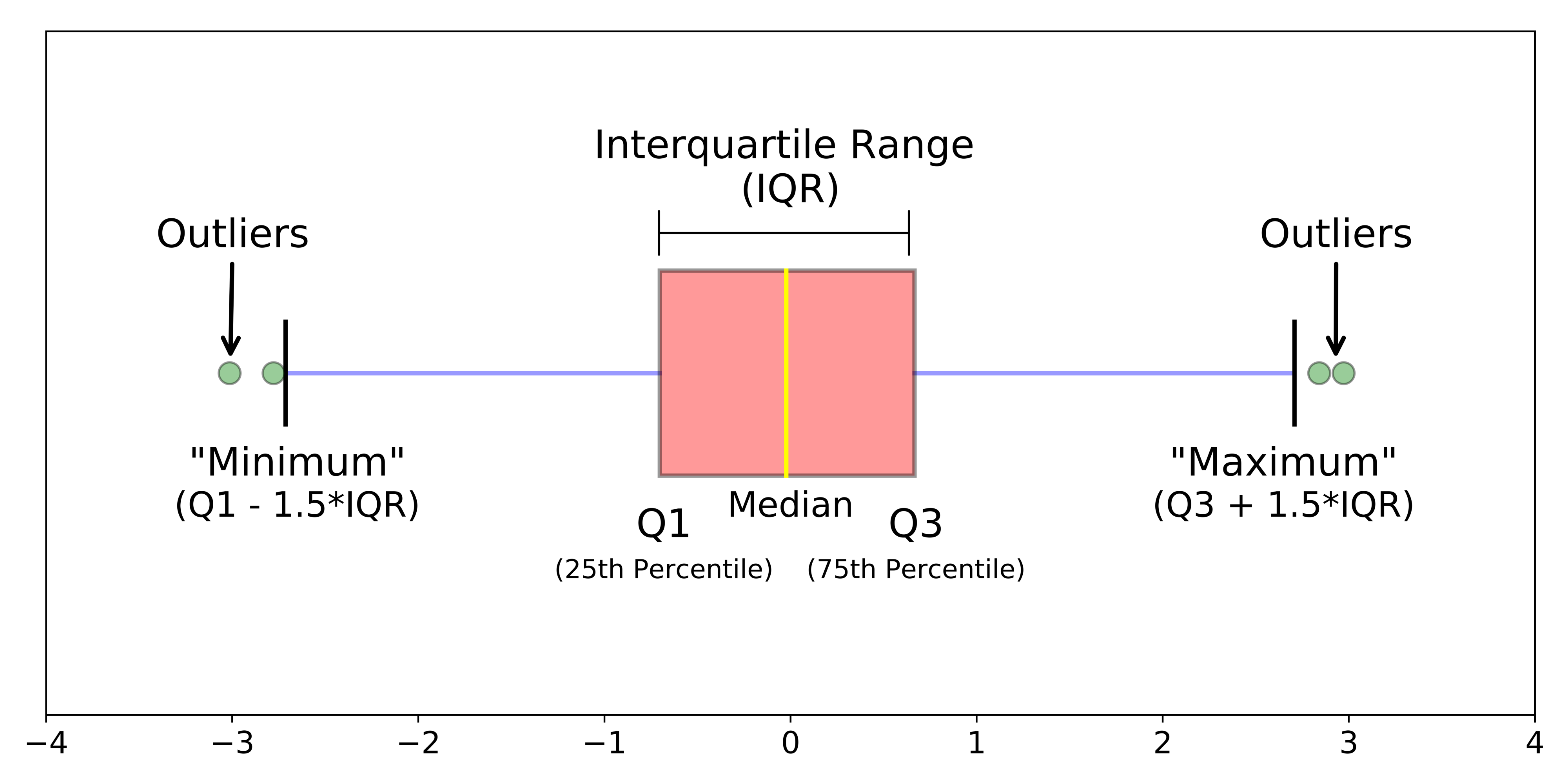
Outlier

Observação coletado de forma errônea ou devido à arredondamentos

Gráfico de caixas (Box plot)

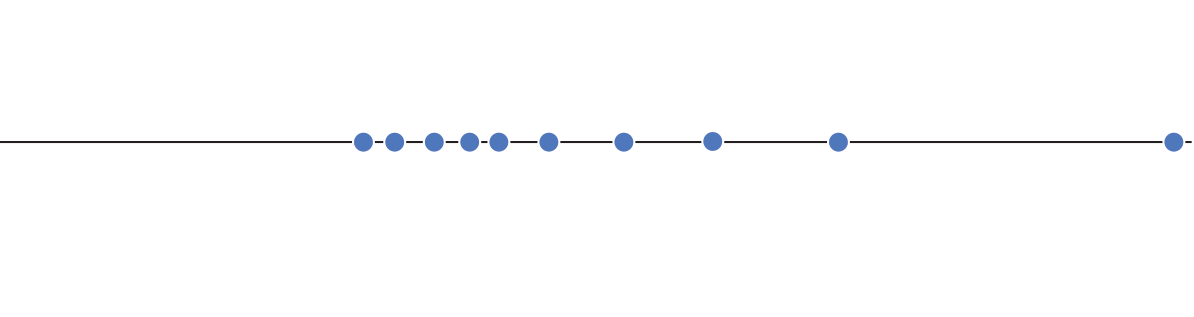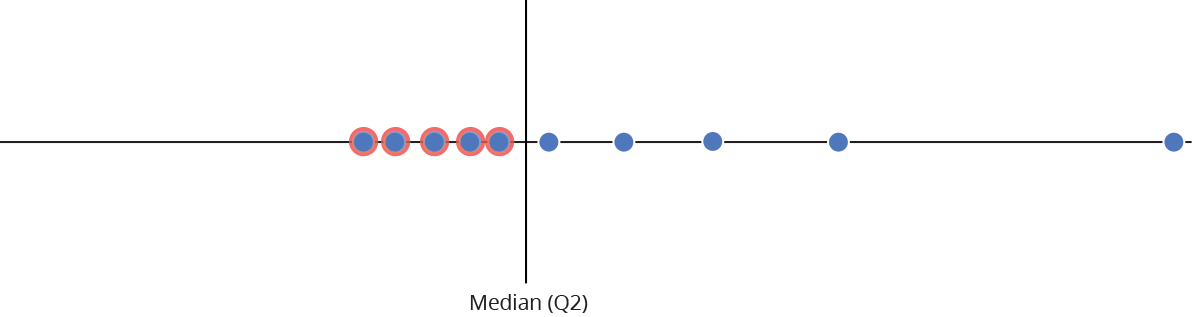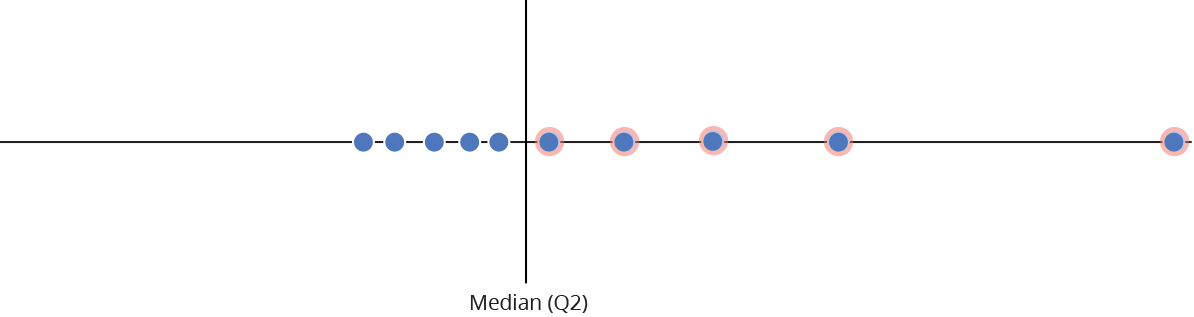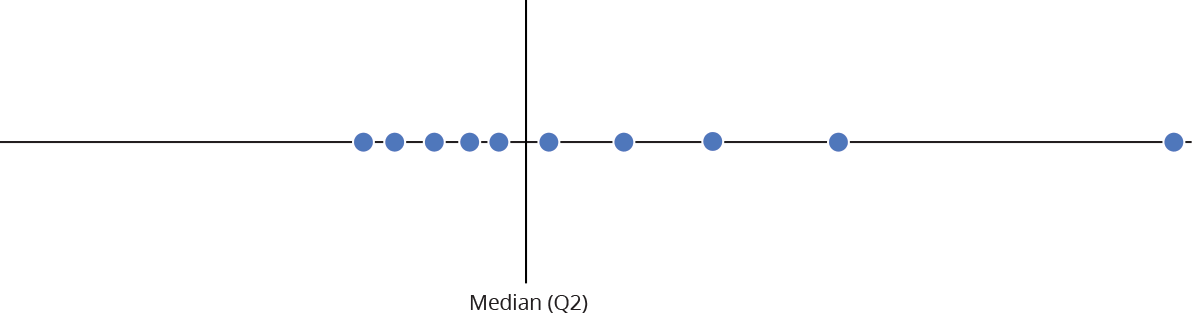
Gráfico de caixas (Box plot)

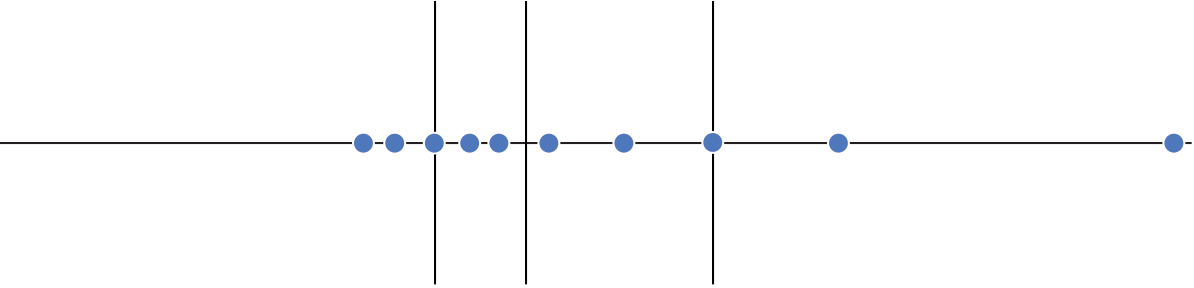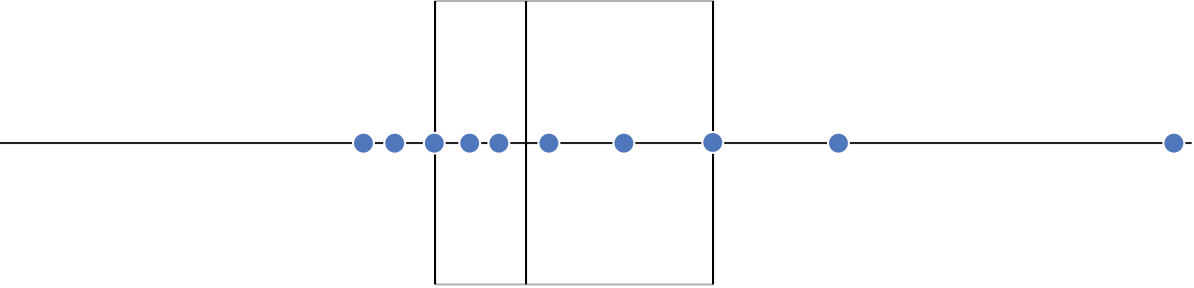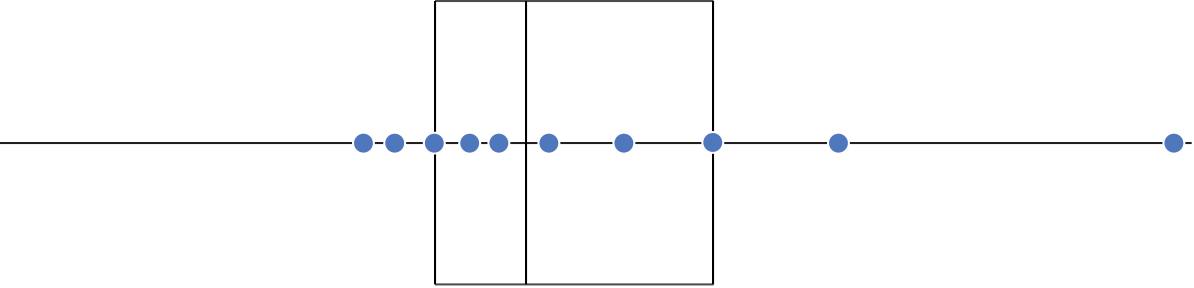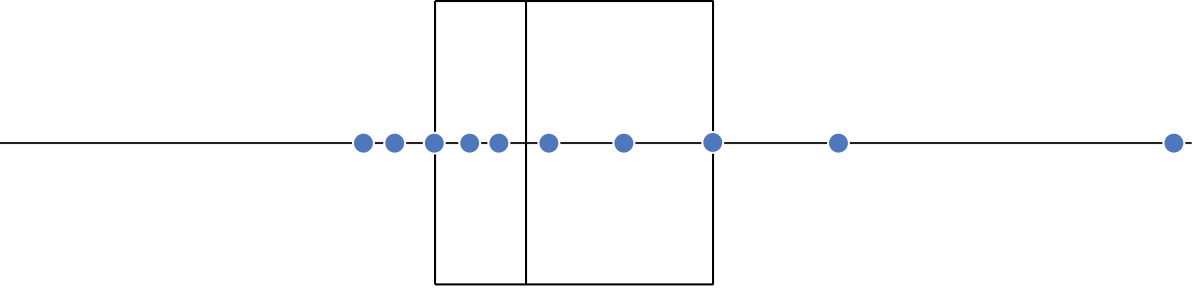
Gráfico de caixas (Box plot)

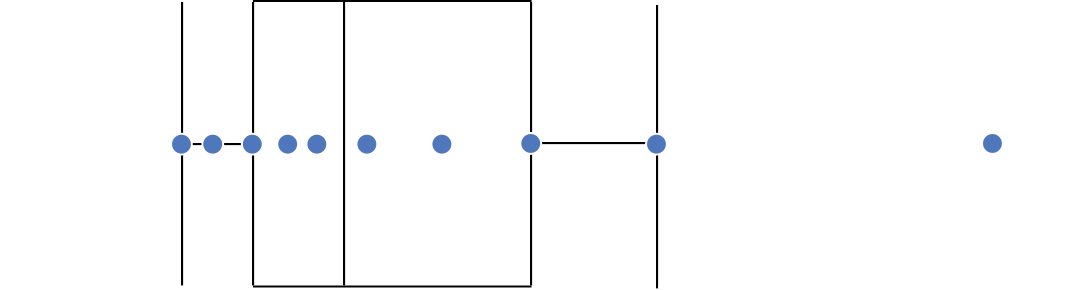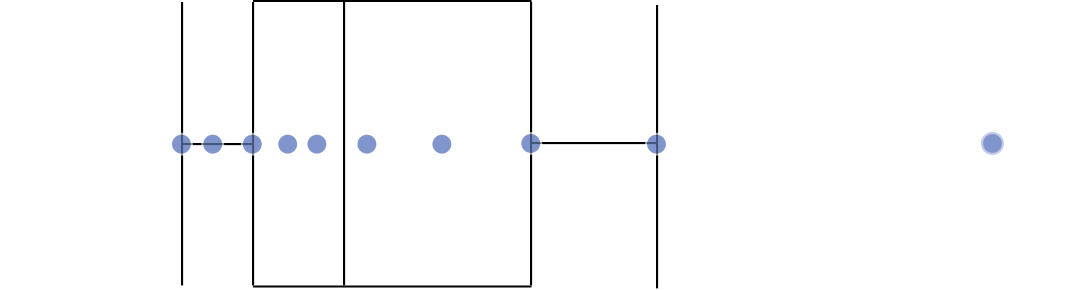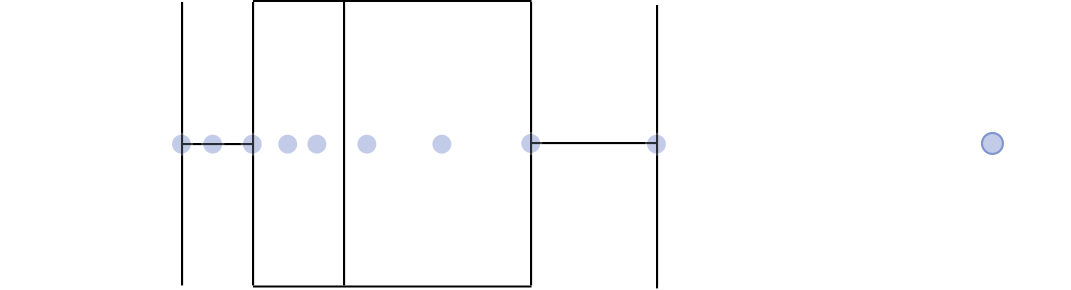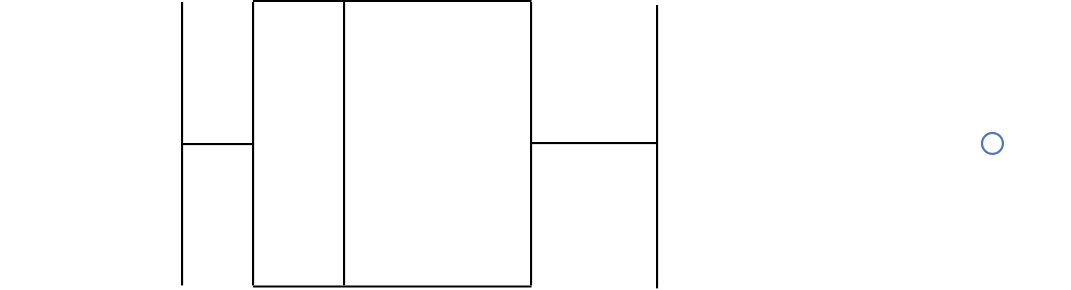
Gráfico de caixas (Box plot)

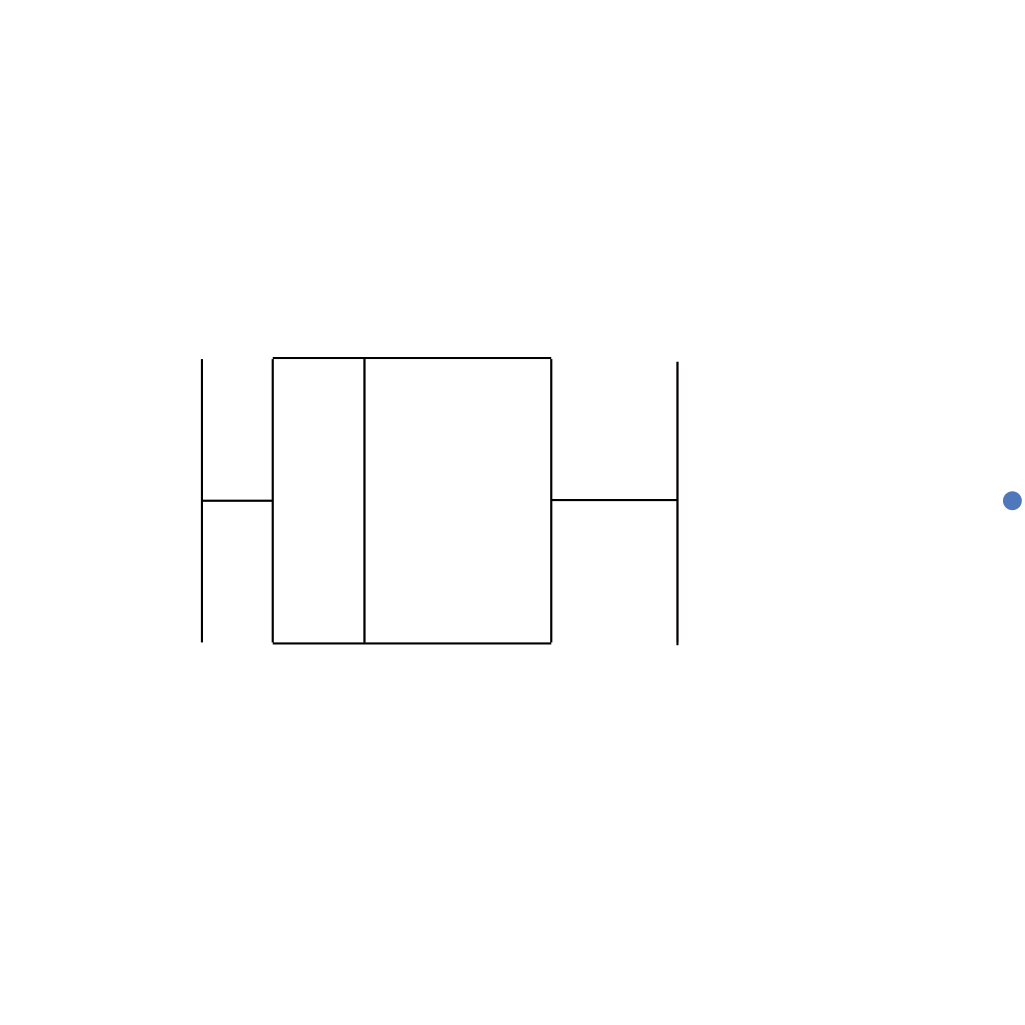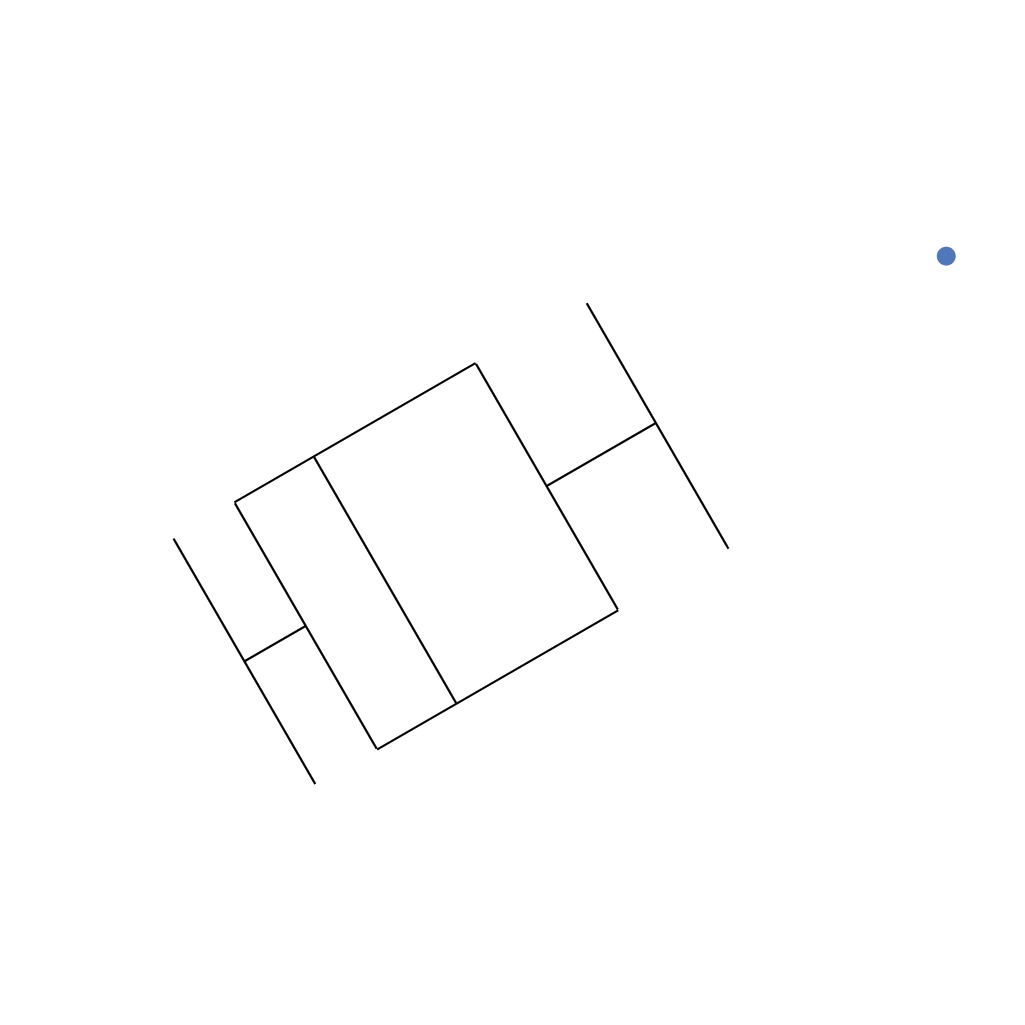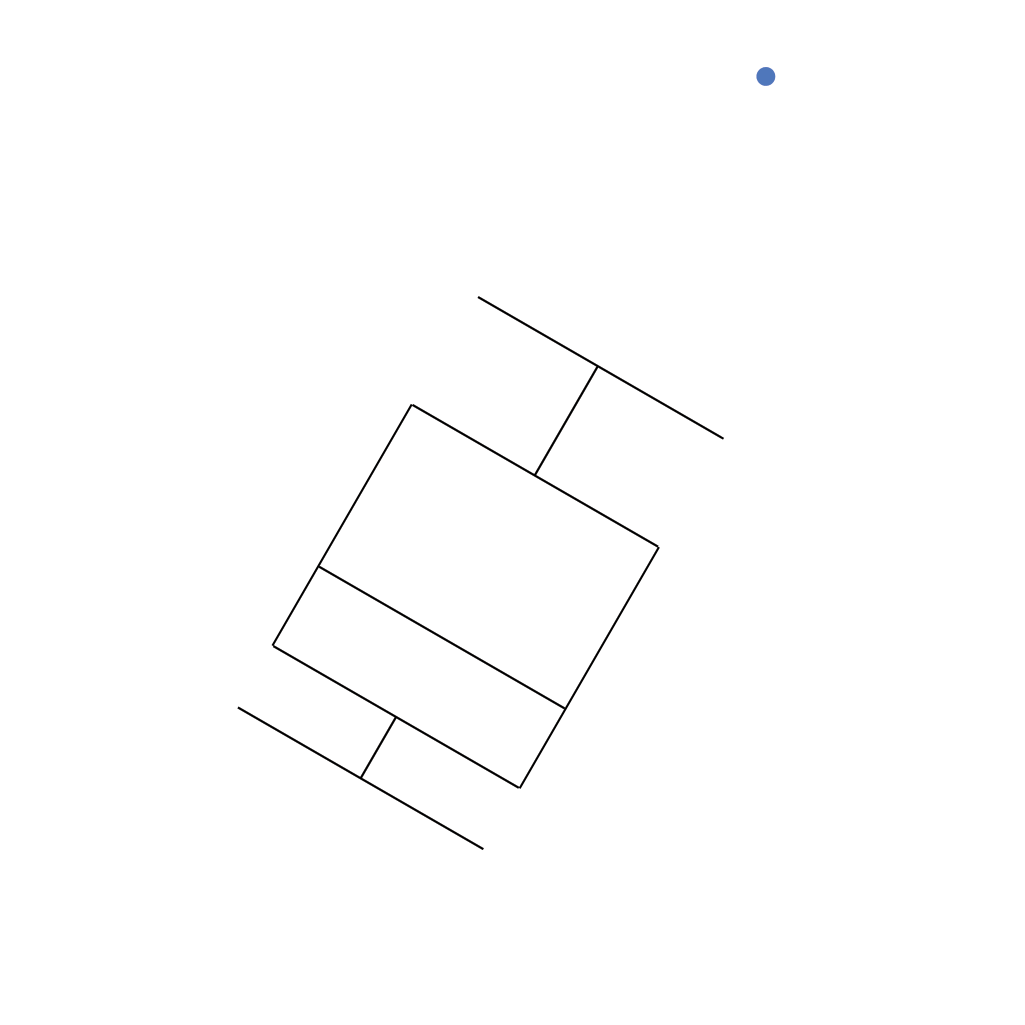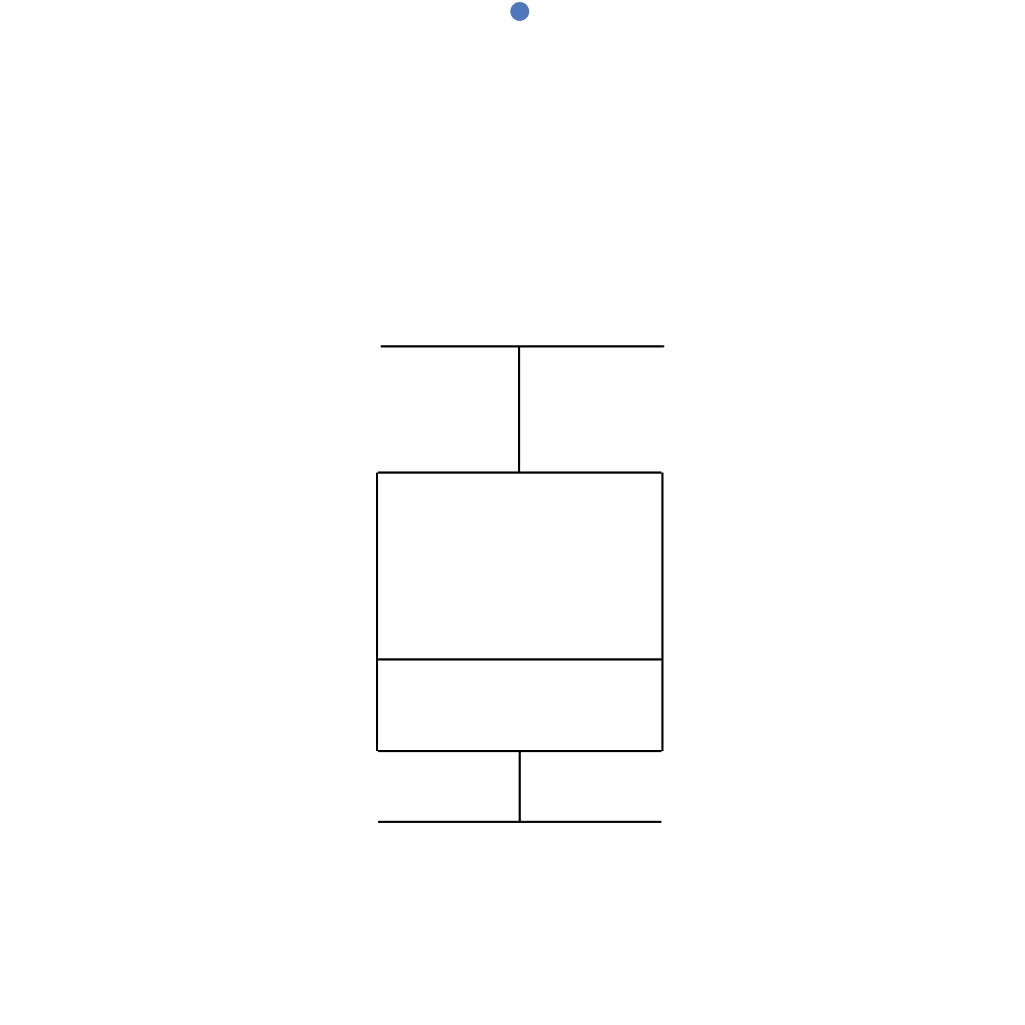
Gráfico de caixas (Box plot)

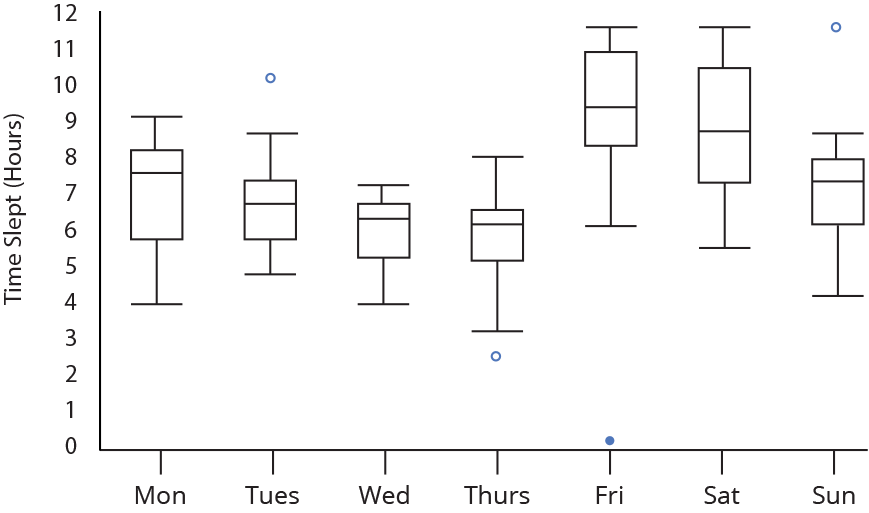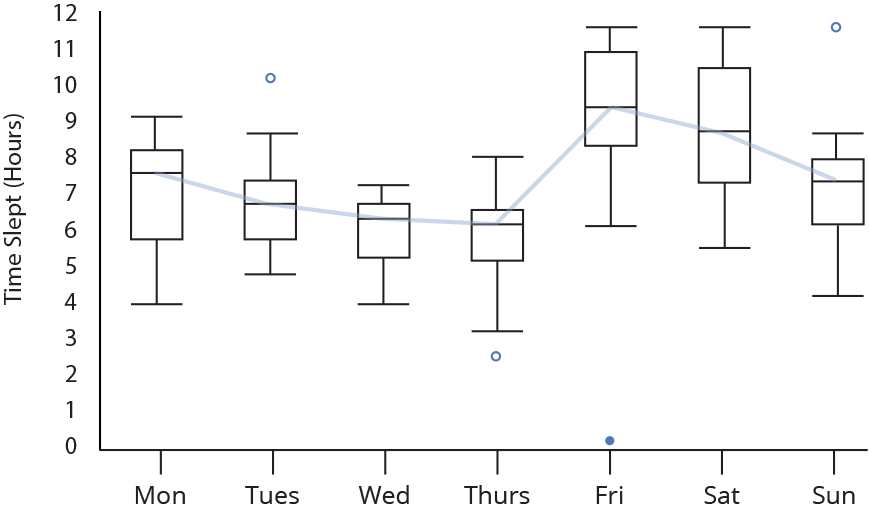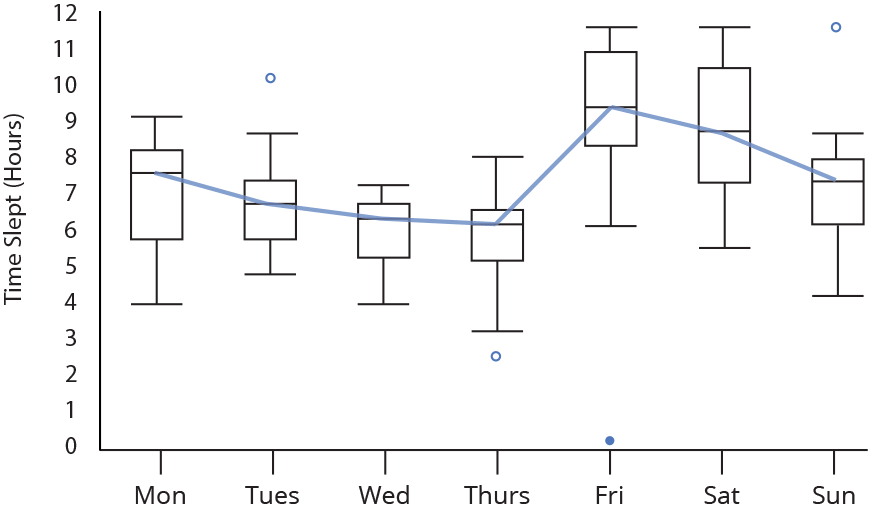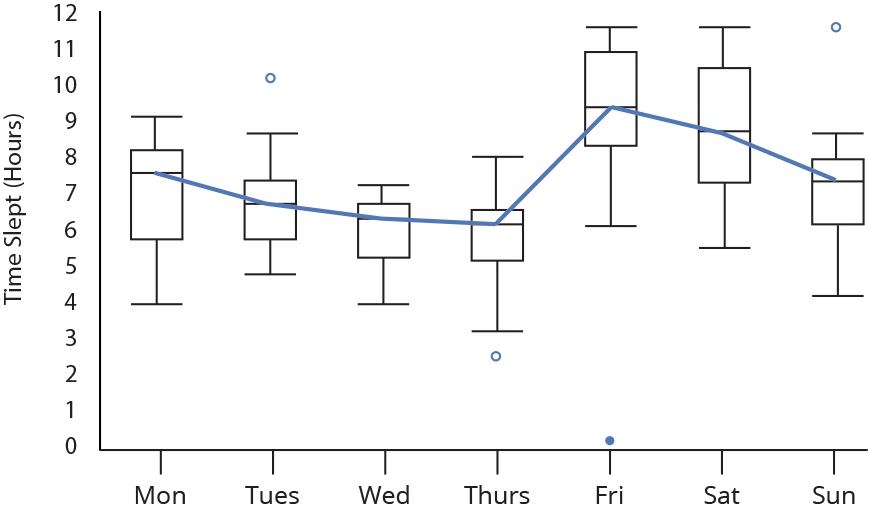
Dúvidas?

3. Análise de dados univariados

Pergunta e hipótese

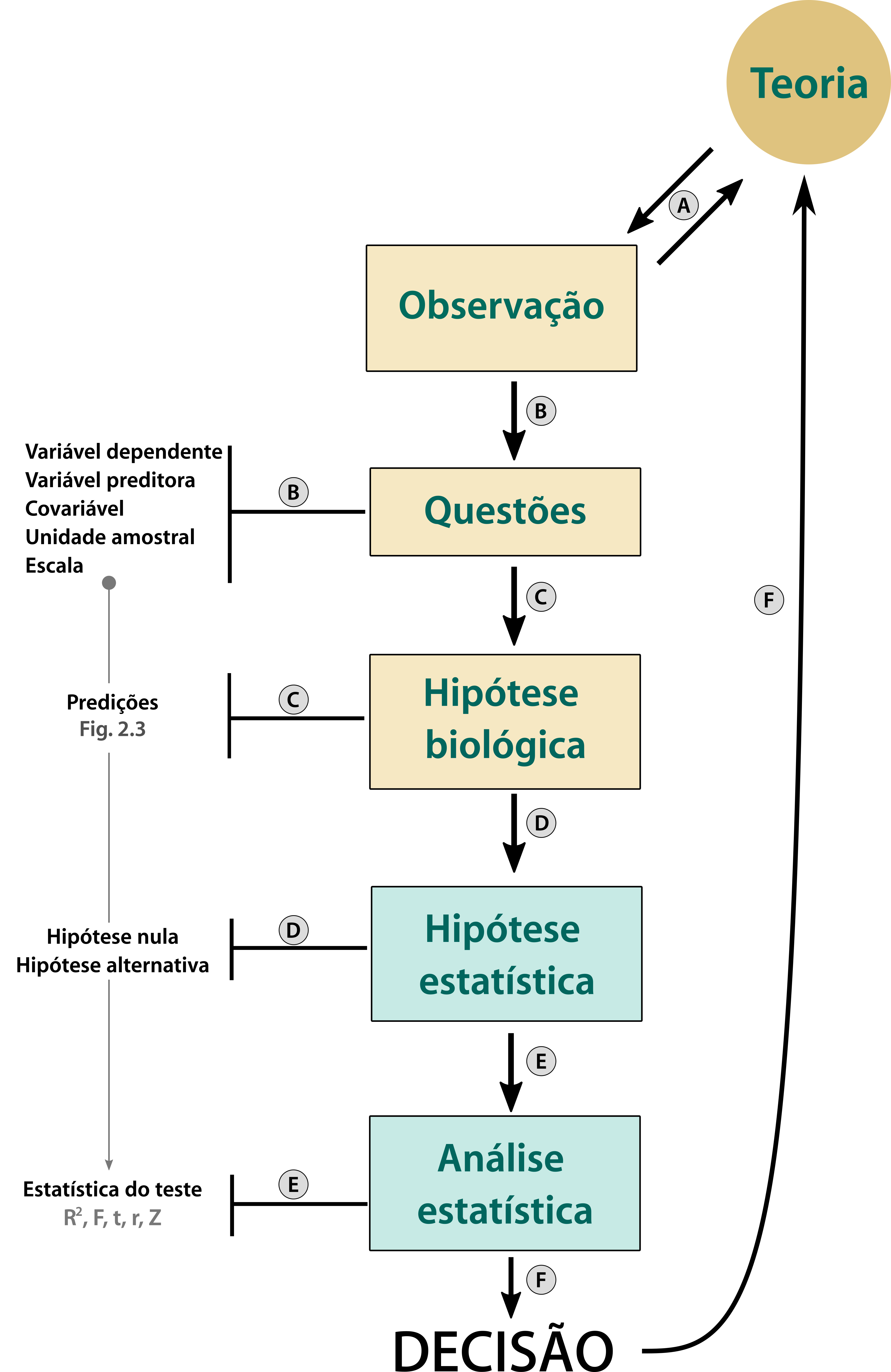
Método hipotético-dedutivo

A. Teoria ecológica/biológica

B. Desenho amostral (variáveis, unidade amostral, esforço, escala - temporal e espacial)

C. Hipótese ecológica/biológica e predições

D. Hipótese estatística - hipótese nula (H0) e hipótese alternativa (H1)

E. Análise estatística - inferência (estatística ou estimador): p, R², F, t, z, r…

F. Decisão: interpretação à luz da teoria ecológica/biológica

Hipótese ecológica e estatística

População e amostra

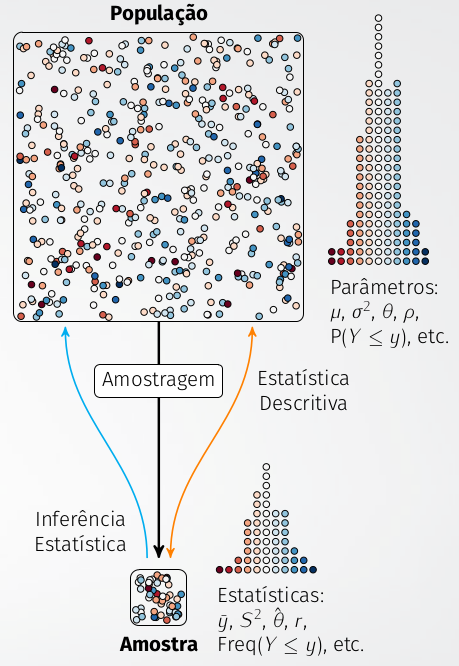
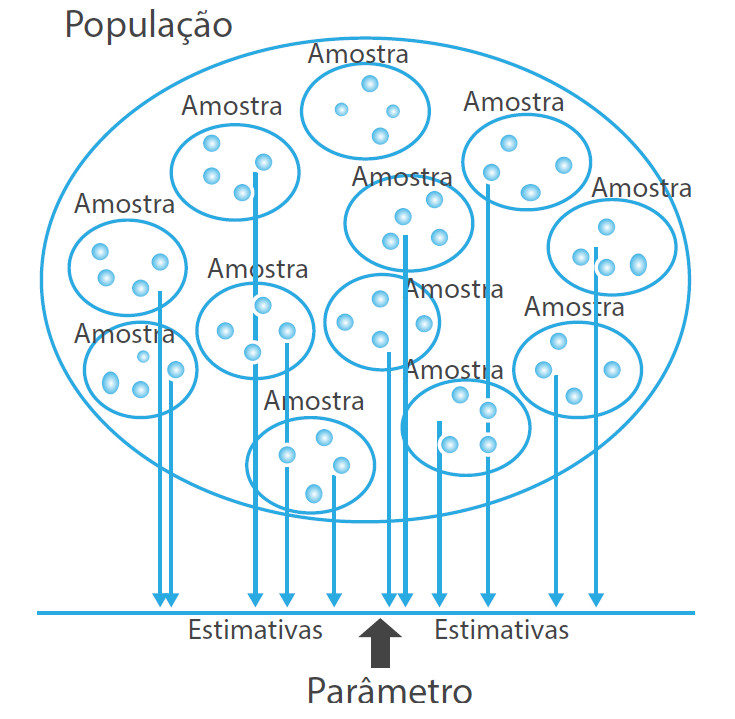
• População: todos dados existentes

• Amostra: parte dos dados coletados

• Amostragem: processo de coleta de dados

• Estatística descritiva: análise descritiva dos dados coletados (medidas-resumo, tabela e gráficos)

• Inferência estatística: análise inferencial da amostra para afirmar algo sobre a população (testes estatísticos)

• Parâmetros: medidas sobre a população (média, variância, desvio padrão) (letras gregas)

• Estatísticas (estimadores): medidas sobre a amostra (média, variância, desvio padrão, erro padrão) (letras romanas)

Parâmetro e estatística (estimador)

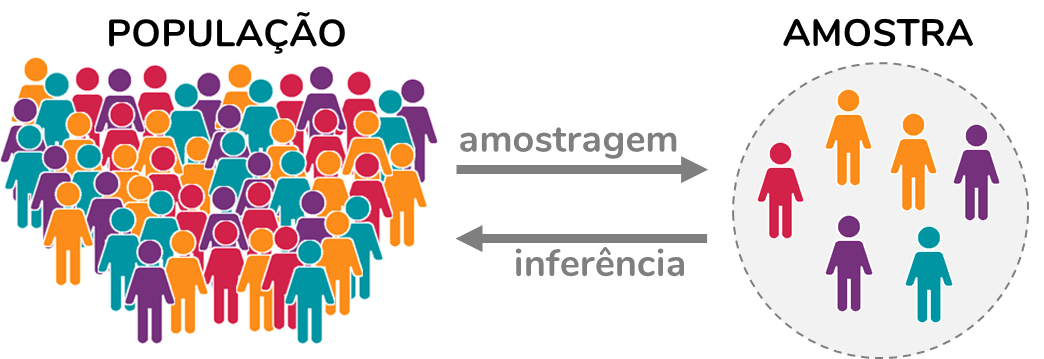
Média

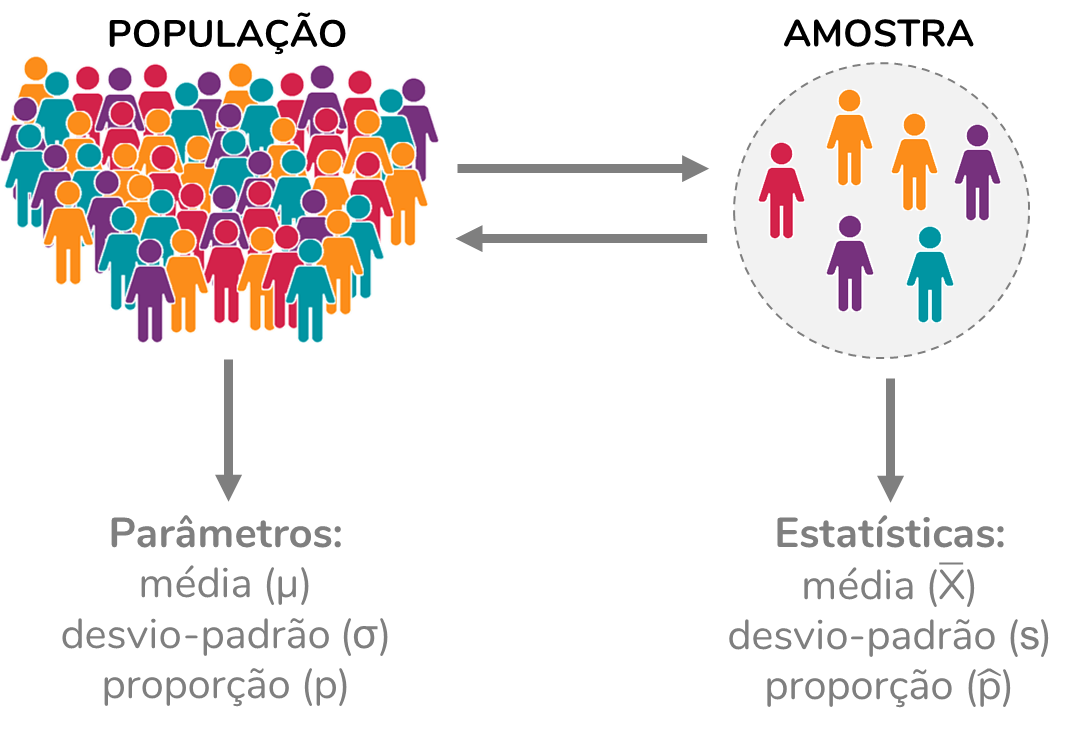
Média da população (parâmetro)

\[\mu=\sum \frac{x_{i}}{n}\]

Média da amostra (estatística)

\[\bar{x}=\sum \frac{x_{i}}{n}\]

# media
amostra <- c(3, 1, 3, 5, 6, 7)
mean(amostra)

[1] 4.166667

Variância

Variância da população (parâmetro)

\[\sigma^2=\sum \frac{(x_{i}-\bar{x})^2}{n}\]

Variância da amostra (estatística)

\[s^2=\sum \frac{(x_{i}-\bar{x})^2}{n}\]

# variancia
amostra <- c(3, 1, 3, 5, 6, 7)
var(amostra)

[1] 4.966667

Desvio padrão

Desvio padrão da população (parâmetro)

\[\sigma =\sqrt {\sum \frac{(x_{i}-\bar{x})^2}{n}}\]

Desvio padrão da amostra (estatística)

\[s =\sqrt {\sum \frac{(x_{i}-\bar{x})^2}{n}}\]

# desvio padrao
amostra <- c(3, 1, 3, 5, 6, 7)
sd(amostra)

[1] 2.228602

Erro padrão

• Erro padrão da média amostral

• Variação da média amostral em relação à média populacional (confiabilidade da média amostral)

\[s_\bar{x} =\frac{s}{\sqrt{n}}\]

# erro padrao da media
amostra <- c(3, 1, 3, 5, 6, 7)
sd(amostra)/sqrt(length(amostra))

[1] 0.9098229

Inferência estatística

Conclusões sobre características da população (parâmetros) através de estatísticas (estimadores) calculadas a partir da(s) amostra(s)

Inferência estatística

Duas categorias:

1. Estimação pontual com um intervo (intervalo de confiança)
2. Testes de hipóteses (testar afirmações)

Intervalo de confiância (IC)

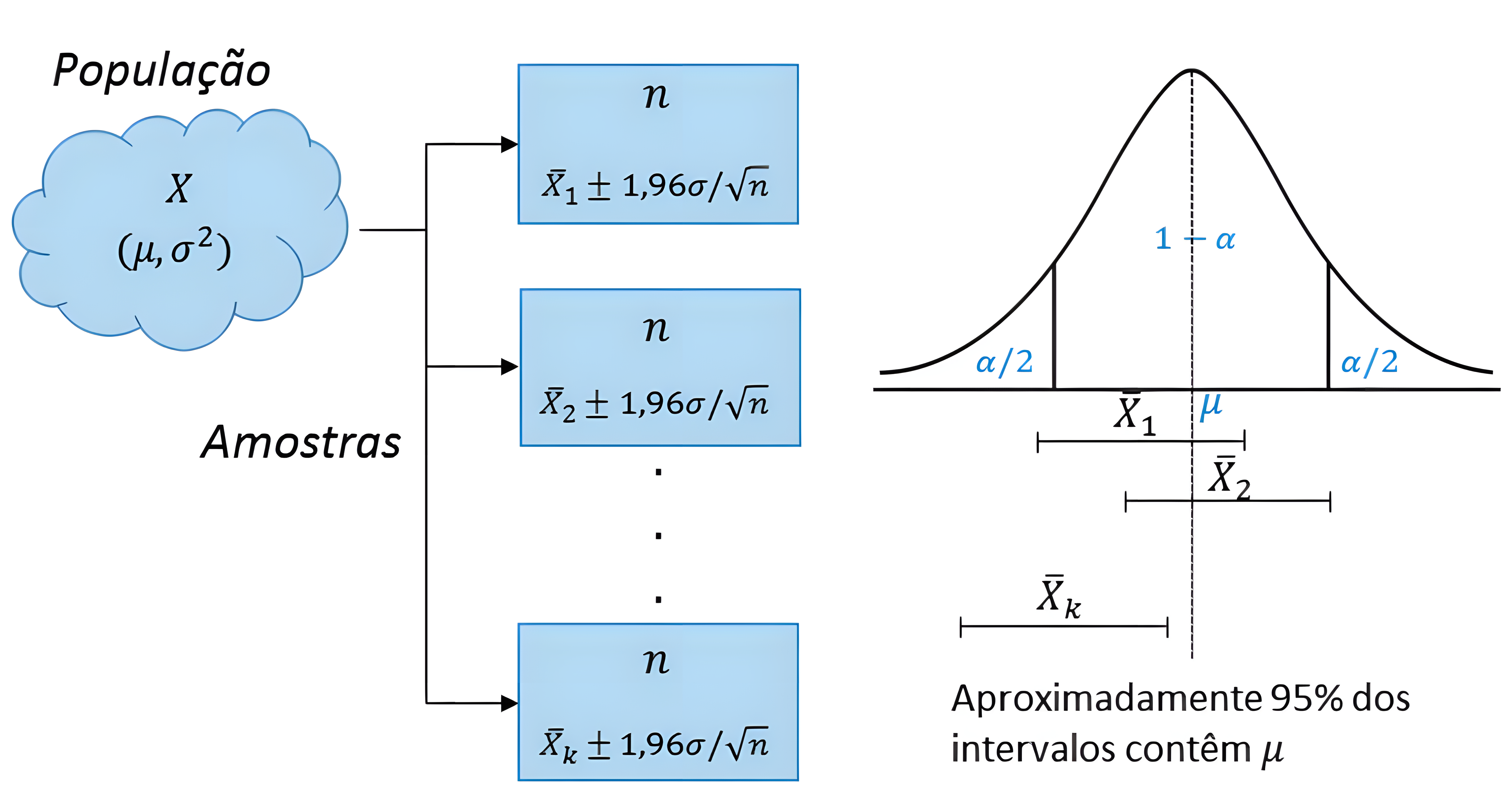
• Intervalo de valores com alta probabilidade (grau de confiança) de conter o valor do parâmetro da população

Intervalo de confiância = [Estivativa pontual ± Erro da estimativa]

• Grau de confiança: probabilidade do intervalo de confiança conter o parâmetro populacional (1−α)

• α: probabilidade de erro ao se afirmar que o intervalo contém o valor do parâmetro

• Ex. A estimativa da média foi 2.5 ± 0.5 para um nível de significância de 5% (α = 0.05)

Intervalo de confiância (IC)

1. Variância σ² da população é conhecida

Erro segue a distribuição z normal padronizada (μ = 0 e σ² = 1)

\[IC^{\mu}_{100(1 - \alpha)\%} = (\bar{x} - z_{\alpha/2}\times\frac{\sigma}{\sqrt{n}}; \bar{x} + z_{\alpha/2}\times\frac{\sigma}{\sqrt{n}}); z_{\alpha/2} = 1.96\]

Ex.: x=10 (amostra), n=100 (amostra), σ=2 (população), α=5%

\[IC^{\mu}_{95} = (10 - 1.96\times\frac{2}{\sqrt{100}}; 10 + 1.96\times\frac{2}{\sqrt{100}})\]

\[IC^{\mu}_{95} = [9.608; 10.392]\]

Distribuição z

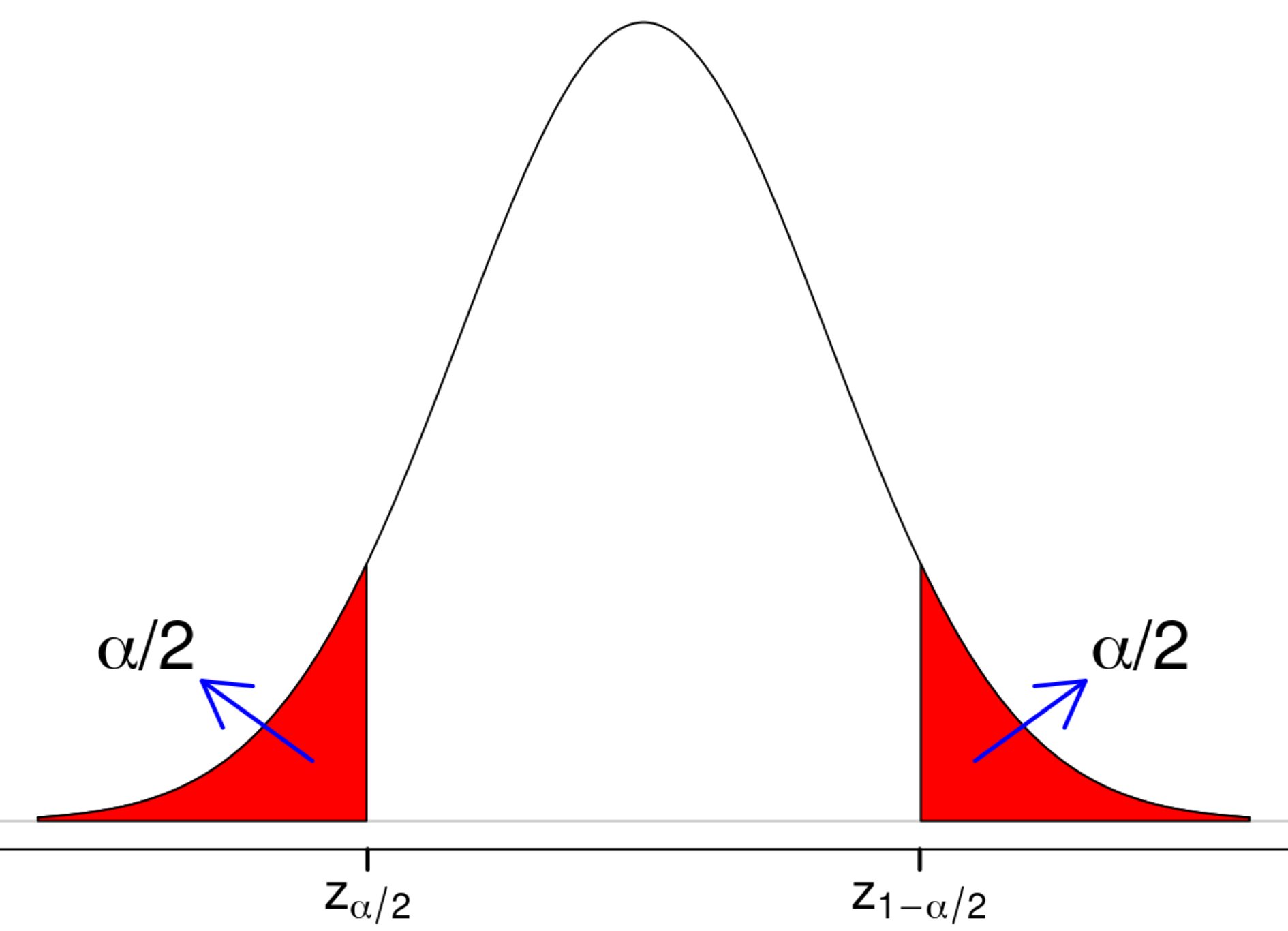
Distribuição de probabilidades de z, com média de z (μ = 0) e desvio padrão de z (σ² = 1)

Como estimamos valores acima e abaixo da média populacional, e para um nível de significância de 5% (α = 0.05), dividimos (α/2 = 0.025) e (1 - α/2 = 0.975)

Intervalo de confiância (IC)

1. Variância σ² da população é conhecida

n <- 100
n

[1] 100

xbar <- 10
xbar

[1] 10

sigma <- 2
sigma

[1] 2

valor_critico <- qnorm(0.975, mean = 0, sd = 1, lower.tail = TRUE)
valor_critico

[1] 1.959964

xbar - valor_critico * (sigma/sqrt(n))

[1] 9.608007

xbar + valor_critico * (sigma/sqrt(n))

[1] 10.39199

Intervalo de confiância (IC)

2. Variância σ² da população é desconhecida

Erro segue a distribuição t

• Variância amostral (s²) ou desvio padrão amostral (s)
• Graus de liberdade (n - 1), sendo n o número de observações

\[IC^{\mu}_{100(1 - \alpha)\%} = (\bar{x} - t_{(n - 1, \alpha/2)}\times\frac{s}{\sqrt{n}}; \bar{x} + t_{(n - 1,\alpha/2)}\times\frac{s}{\sqrt{n}})\]

\[s = \sqrt\frac{\sum_{i = 1}^n{(x_i - \bar{x})^2}}{n - 1}\]

Distribuição t

Graus de liberdade (g.l.): quantidade de observações (n) menos a quantidade de parâmetros estimados (μ)

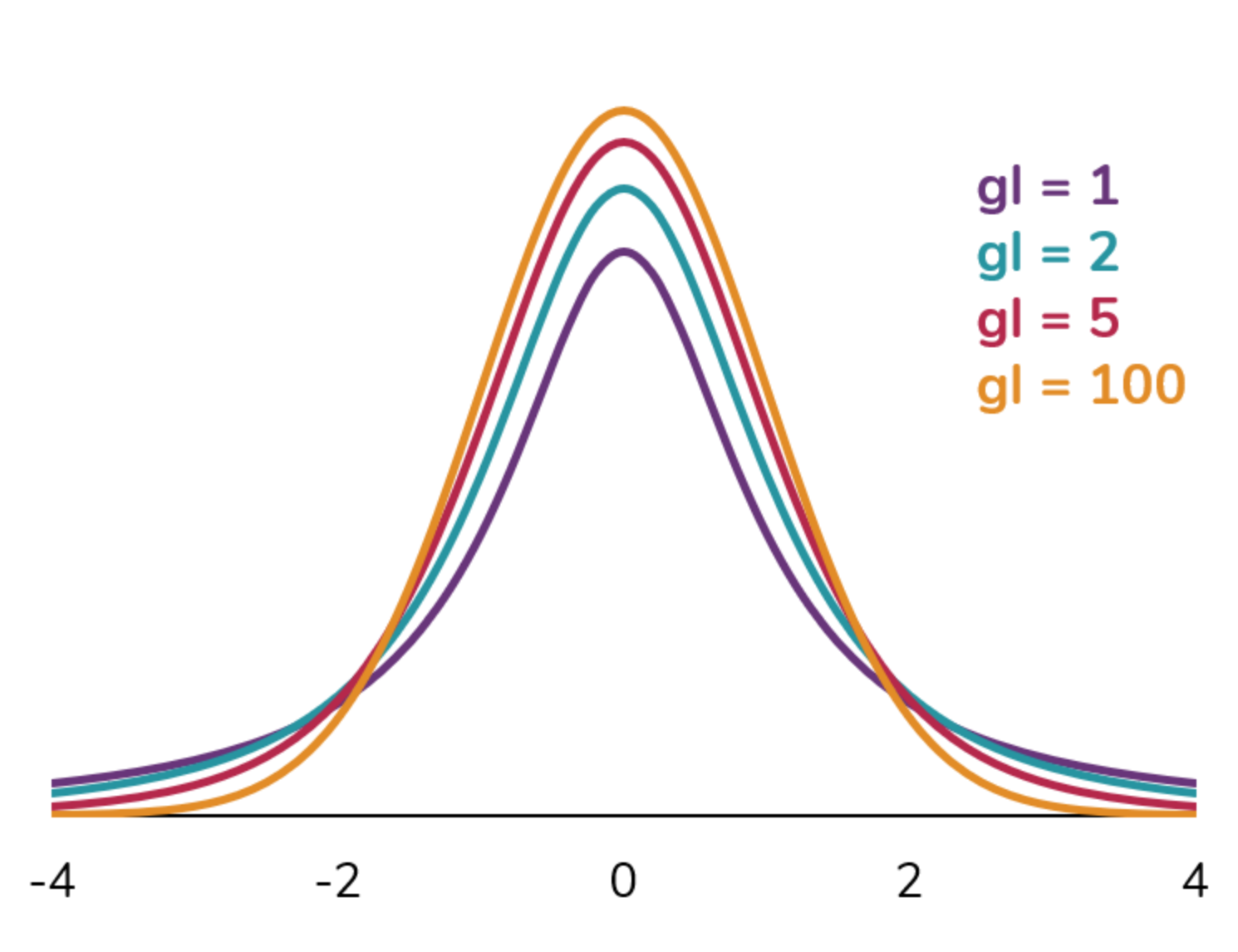
Intervalo de confiância (IC)

2. Variância σ² da população é desconhecida

Ex.: [36.4, 35.7, 37.2, 36.5, 34.9, 35.2, 36.3, 35.8, 36.6, 36.9]

\[\bar{x} = \frac{\sum_{i=1}^n x_i}{n} = 36.15\] \[s = \sqrt\frac{\sum_{i = 1}^n{(x_i - \bar{x})^2}}{n - 1} = \sqrt\frac{4.865}{9} = 0.7352\] \[t_{(n−1,α/2)} = t_{(9,0.025)} = 2.26\]

Intervalo de confiância (IC)

2. Variância σ² da população é desconhecida

Ex.: [36.4, 35.7, 37.2, 36.5, 34.9, 35.2, 36.3, 35.8, 36.6, 36.9]

\[IC^{\mu}_{95} = (36.15 - 2.26\times\frac{0.7352}{\sqrt{10}}; 36.15 + 2.26\times\frac{0.7352}{\sqrt{10}})\]

\[IC^{\mu}_{95} = [35.624; 36.676]\]

Intervalo de confiância (IC)

2. Variância σ² da população é desconhecida

amostra <- c(36.4, 35.7, 37.2, 36.5, 34.9, 35.2, 36.3, 35.8, 36.6, 36.9)

n <- length(amostra)
n

[1] 10

xbar <- mean(amostra)
xbar

[1] 36.15

s <- sd(amostra)
s

[1] 0.7352248

valor_critico <- qt(df = n - 1, p = 0.975)
valor_critico

[1] 2.262157

xbar - valor_critico * (s/sqrt(n))

[1] 35.62405

xbar + valor_critico * (s/sqrt(n))

[1] 36.67595

Dúvidas?

Teste de hipóteses

Regra de decisão para rejeitar (ou não) uma afirmação (hipótese) feita sobre um parâmetro populacional desconhecido, com base numa amostra aleatória

Ex:

• Testar se agroflorestas retêm mais caborno que a agricultura convencional
• Verificar se paisagens mais fragmentadas possuem menos espécies
• Testar se as pessoas gostam mais de Harry Potter ou Senhor dos Anéis

Teste de hipóteses

Regra de decisão para rejeitar (ou não) uma afirmação (hipótese) feita sobre um parâmetro populacional desconhecido, com base numa amostra aleatória

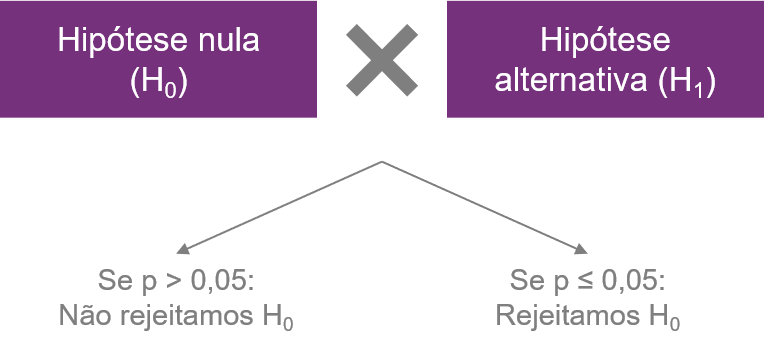
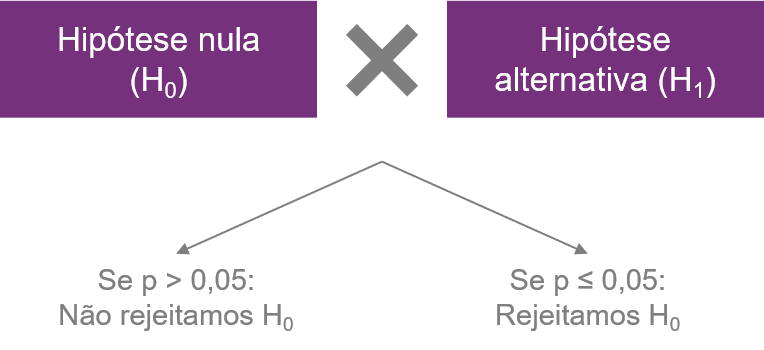
Hipótese Nula (H0): hipótese a ser testada

Hipótese Alternativa (H1): hipótese a ser confrontada com H0

• Teste feito para concluir na rejeição (ou não) de H0
• Decisão é feita com base em informações de uma amostra, estaremos sujeitos a dois tipos de erros

Teste de hipóteses

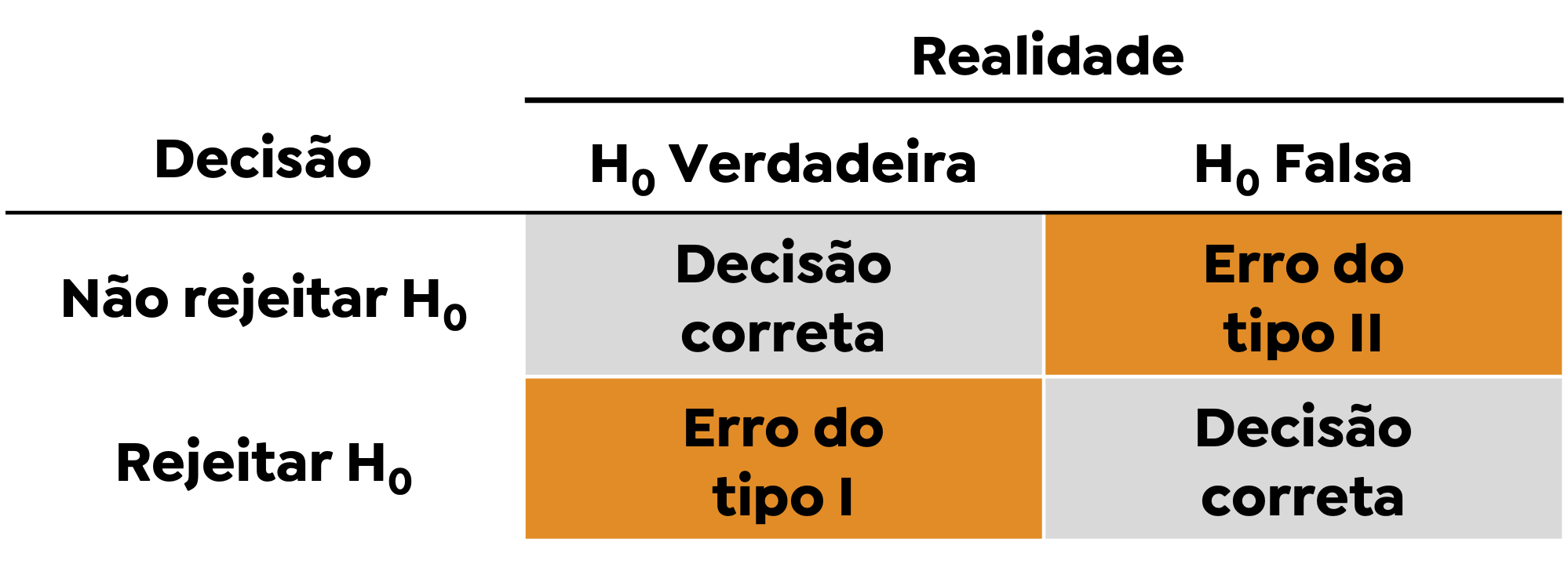
Erros

• Erro do tipo I: rejeitar H0 quando H0 é verdadeira

α = P(erro do tipo I) = P(rejeitar H0|H0 é verdadeira)

• Erro do tipo II: não rejeitarmos H0 quando H0 é falsa

β = P(erro do tipo II) = P(não rejeitar H0|H0 é falsa)

Teste de hipóteses

Etapas

1. Definir as hipóteses nula (H0) e alternativa (H1)
2. Fixar o nível de significância (α) (e.g. α = 5% ou 0.05)
3. Determinar a estatística do teste (e.g. t)
4. Determinar a região crítica do teste (RC)
5. Calcular o valor da estatística do teste (amostra)
6. Se o valor calculado no passo 5 pertence à RC, rejeita-se H0, se não pertencer, não se rejeita H0
7. Conclusão do teste

Teste de hipóteses

Detalhamento

1 Definição das hipóteses

H0: µ = µ0
H1: µ ≠ µ0

H0: µ = µ0
H1: µ < µ0

H0: µ = µ0
H1: µ > µ0

2. Fixar o nível de significância α (5% ou 0.05)

3. Definir a estatística de teste (t)

\[t = \frac{\bar{x} - \mu}{s / \sqrt{n}} \sim t_{n - 1}\]

Teste de hipóteses

Detalhamento

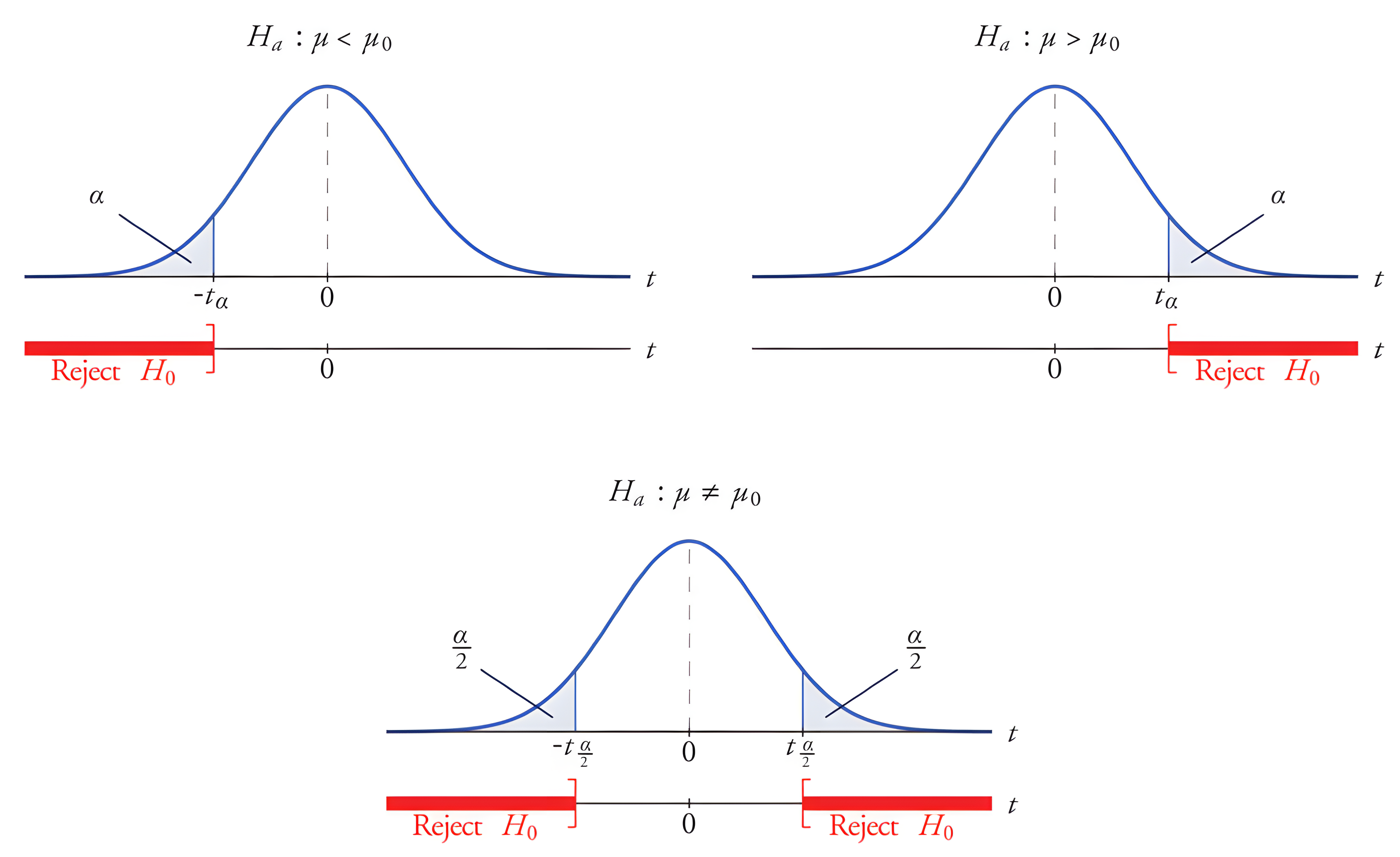
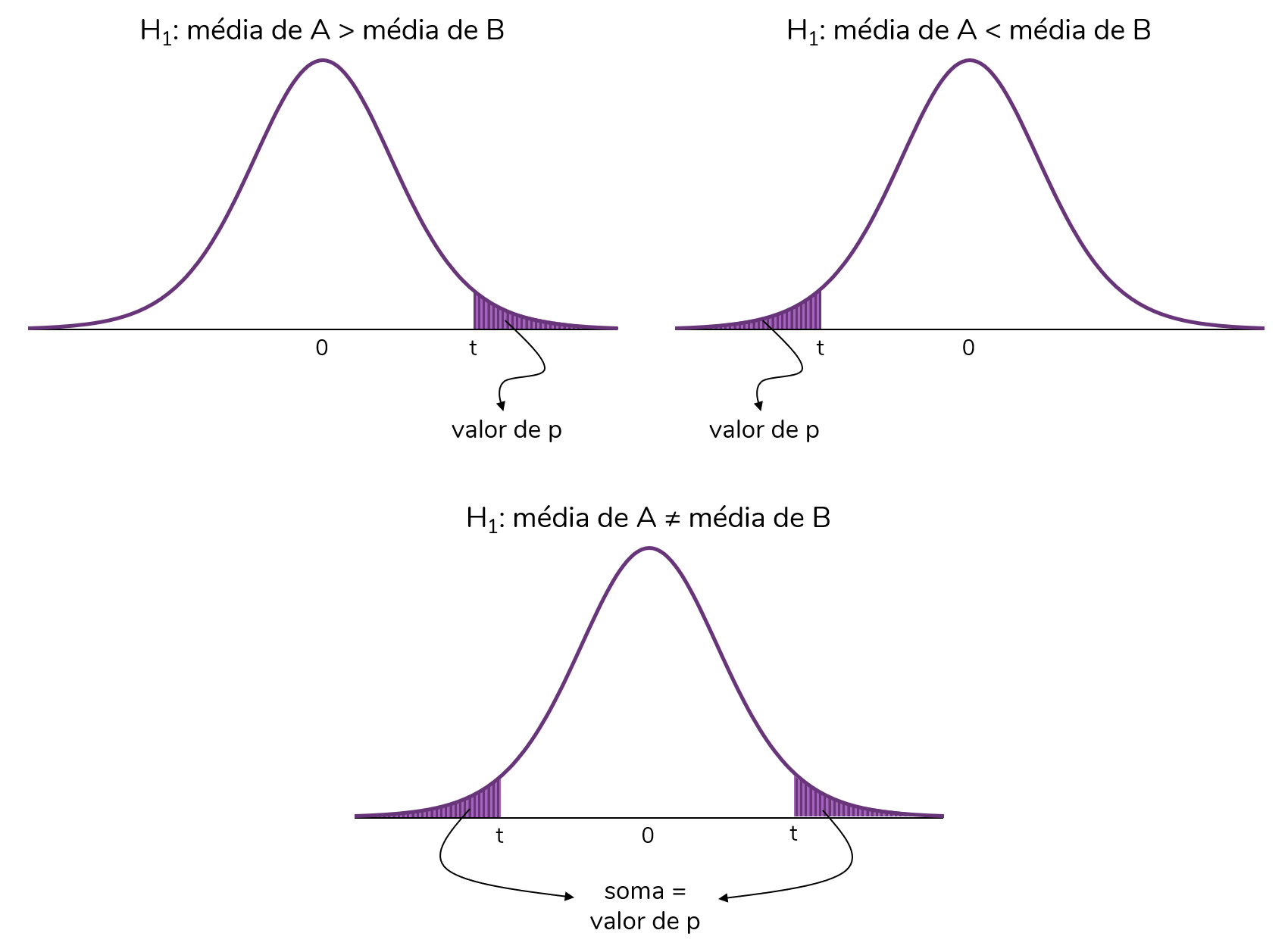
4 Definir a região crítica (RC)

H0: µ = µ0
H1: µ ≠ µ0

H0: µ = µ0
H1: µ < µ0

H0: µ = µ0
H1: µ > µ0

Teste de hipóteses

Detalhamento

5. Com base nos valores observados da amostra, calcular o valor da estatística do teste t

\[t_c = \frac{\bar{x} - \mu_0}{s/\sqrt{n}}\]

6. Se tc ∈ RC ⇒ rejeitar H0 (corrobora H1)
   Se tc ∉ RC ⇒ não rejeitar H0 (não corrobora H1)

7. Concluir sobre a decisão tomada no passo 6

Teste de hipóteses

Exemplo

Medimos a altura de 25 bananeiras adultas num SAF. Sabemos que num cultivo convencional, as bananeiras adultas chegam a 3 metros. Considerando um nível de significância de 5%, podemos dizer que, em média, as bananeiras crescem mais no SAF?

altura = [4.3, 2.6, 4.4, 3.0, 2.7, 2.9, 3.3, 2.7, 4.3, 3.8, 3.1, 2.5, 4.3, 4.2, 4.0, 4.2, 3.3, 3.2, 3.4, 4.5, 3.5, 2.6, 2.5, 2.5, 4.2]

Teste de hipóteses

Exemplo

1. As hipóteses que queremos testar são:

H0: µ = 3 contra H1: µ > 3

2. Fixamos α = 0.05

3. A estatística de teste é a t

\[t = \frac{\bar{x} - \mu}{s / \sqrt{n}} \sim t_{n - 1}\]

Teste de hipóteses

Exemplo

4. A região crítica é do tipo (teste unicaldal à direita)

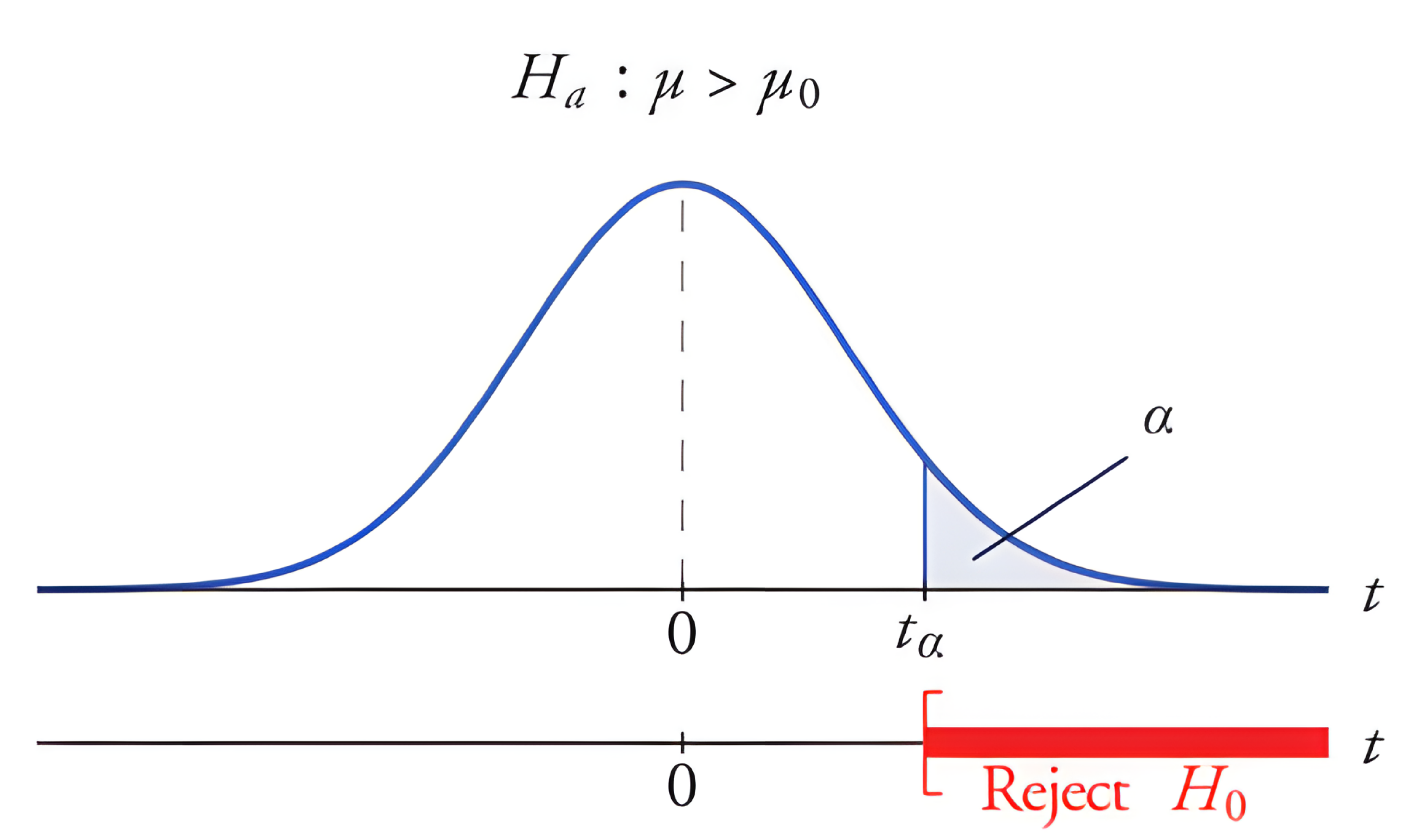
onde t = t(n-1, α) = t(24,0.05) = 1.71 (tabela da distribuição t)

Teste de hipóteses

Exemplo

5. A partir dos dados amostrais temos que

\[t_c = \frac{\bar{x} - \mu_0}{s/\sqrt{n}} = \frac{3.44 - 3}{0.72/\sqrt{25}}=3.0731\]

6. Temos que tc ∈ RC pois 3.0731 > 1.71, portanto, rejeitamos a hipótese nula

7. Com base nos dados amostrais, podemos concluir, ao nível de 5% de significância, que a altura média das bananeiras é maior no SAF do que na agricultura convencional

Teste de hipóteses

Exemplo

# amostra
amostra <- c(4.3, 2.6, 4.4, 3.0, 2.7, 2.9, 3.3, 2.7, 4.3, 3.8, 3.1, 2.5, 4.3, 4.2, 4.0, 4.2, 3.3, 3.2, 3.4, 4.5, 3.5, 2.6, 2.5, 2.5, 4.2)

# numero
n <- length(amostra)
n

[1] 25

# media
xbar <- mean(amostra)
xbar

[1] 3.44

# desvio padrao
s <- sd(amostra)
s

[1] 0.7158911

# regiao critica
rc <- qt(p = 0.95, df = n - 1)
rc

[1] 1.710882

# estistica t
t <- (xbar - 3)/(s/sqrt(n))
t

[1] 3.073093

Teste de hipóteses

Exemplo

# amostra
amostra <- c(4.3, 2.6, 4.4, 3.0, 2.7, 2.9, 3.3, 2.7, 4.3, 3.8, 3.1, 2.5, 4.3, 4.2, 4.0, 4.2, 3.3, 3.2, 3.4, 4.5, 3.5, 2.6, 2.5, 2.5, 4.2)

# teste t
t.test(x = amostra, mu = 3, alternative = "greater")

    One Sample t-test

data:  amostra
t = 3.0731, df = 24, p-value = 0.002607
alternative hypothesis: true mean is greater than 3
95 percent confidence interval:
 3.195039      Inf
sample estimates:
mean of x 
     3.44 

Valor de p

Probabilidade de termos obtido aqueles resultados (ou mais extremos), dado que a H0 é verdadeira

P(resultados | H0 é verdadeira)

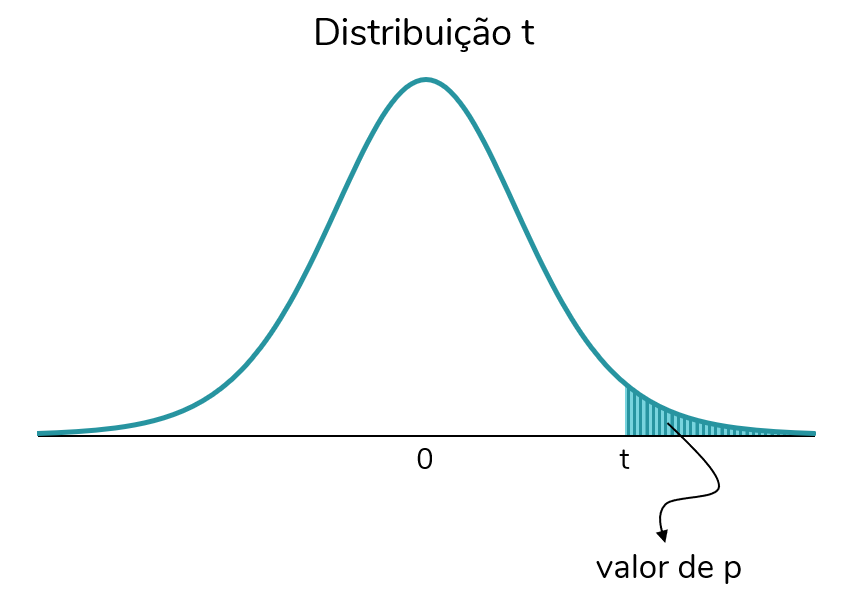
Valor de p

Probabilidade de termos obtido aqueles resultados (ou mais extremos), dado que a H0 é verdadeira

P(resultados | H0 é verdadeira)

Teste t

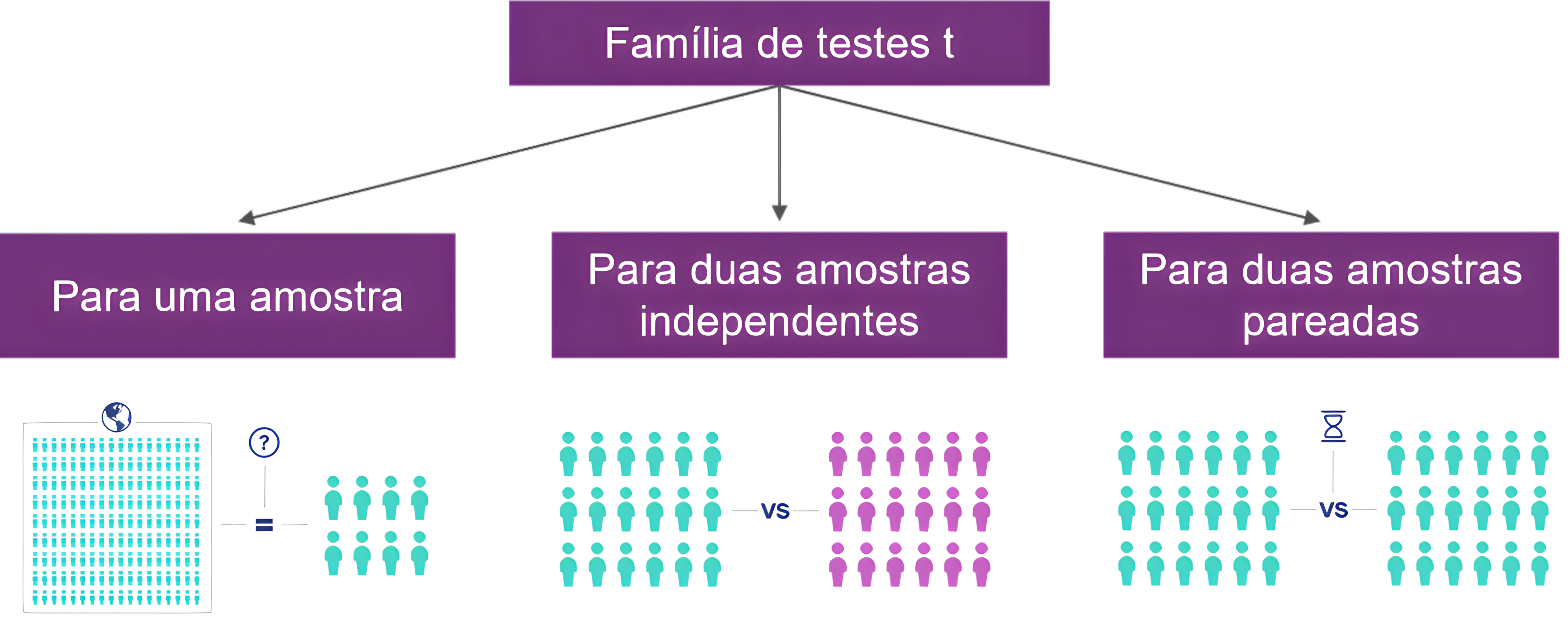
Teste t para uma amostra

One sample t test

Teste t para uma amostra

One sample t test

## maior
# amostra
amostra <- c(4.3, 2.6, 4.4, 3.0, 2.7, 2.9, 3.3, 2.7, 4.3, 3.8, 3.1, 2.5, 4.3, 4.2, 4.0, 4.2, 3.3, 3.2, 3.4, 4.5, 3.5, 2.6, 2.5, 2.5, 4.2)

# teste t
t.test(x = amostra, mu = 3, alternative = "greater")

    One Sample t-test

data:  amostra
t = 3.0731, df = 24, p-value = 0.002607
alternative hypothesis: true mean is greater than 3
95 percent confidence interval:
 3.195039      Inf
sample estimates:
mean of x 
     3.44 

Teste t para uma amostra

One sample t test

## menor
# amostra
amostra <- c(4.3, 2.6, 4.4, 3.0, 2.7, 2.9, 3.3, 2.7, 4.3, 3.8, 3.1, 2.5, 4.3, 4.2, 4.0, 4.2, 3.3, 3.2, 3.4, 4.5, 3.5, 2.6, 2.5, 2.5, 4.2)

# teste t
t.test(x = amostra, mu = 3, alternative = "less")

    One Sample t-test

data:  amostra
t = 3.0731, df = 24, p-value = 0.9974
alternative hypothesis: true mean is less than 3
95 percent confidence interval:
     -Inf 3.684961
sample estimates:
mean of x 
     3.44 

Teste t para uma amostra

One sample t test

## diferente
# amostra
amostra <- c(4.3, 2.6, 4.4, 3.0, 2.7, 2.9, 3.3, 2.7, 4.3, 3.8, 3.1, 2.5, 4.3, 4.2, 4.0, 4.2, 3.3, 3.2, 3.4, 4.5, 3.5, 2.6, 2.5, 2.5, 4.2)

# teste t
t.test(x = amostra, mu = 3, alternative = "two.sided")

    One Sample t-test

data:  amostra
t = 3.0731, df = 24, p-value = 0.005213
alternative hypothesis: true mean is not equal to 3
95 percent confidence interval:
 3.144495 3.735505
sample estimates:
mean of x 
     3.44 

Teste t

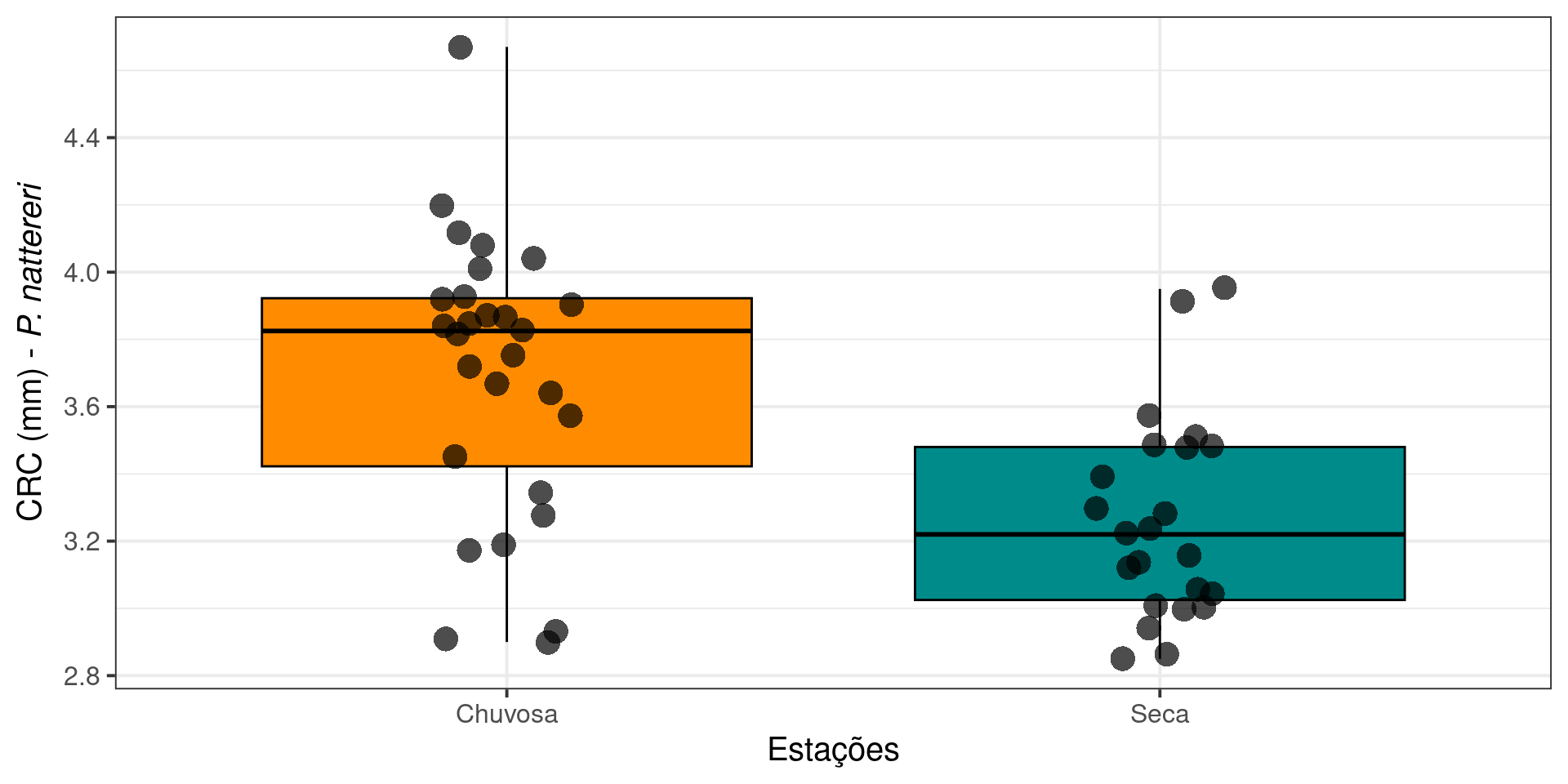
Physalaemus nattereri

Comprimento rostro-cloacal (CRC)

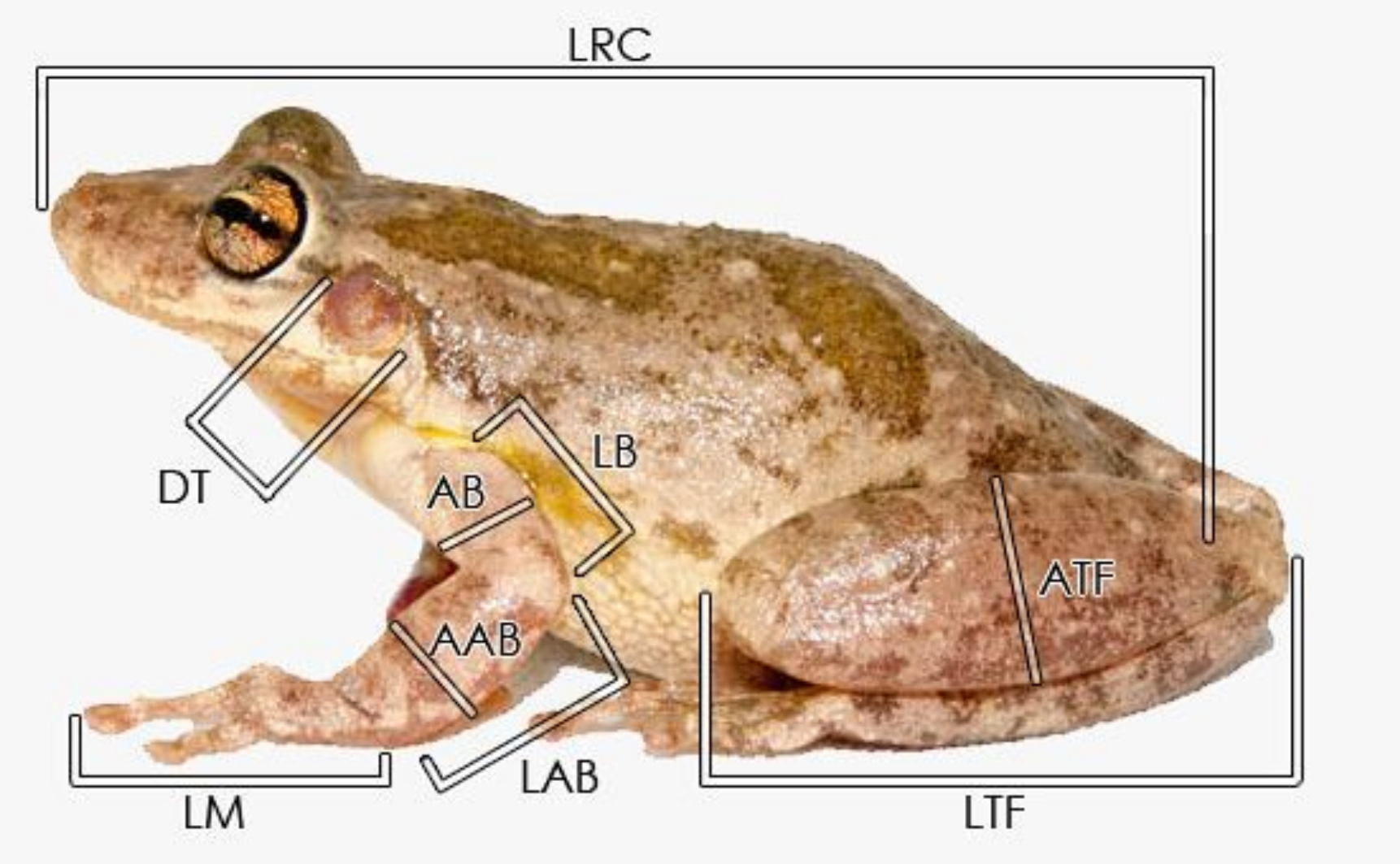
Teste t para duas amostras indep.

Independent-samples t test

Estacao	mean	sd
Chuvosa	3.70	0.42
Seca	3.26	0.30

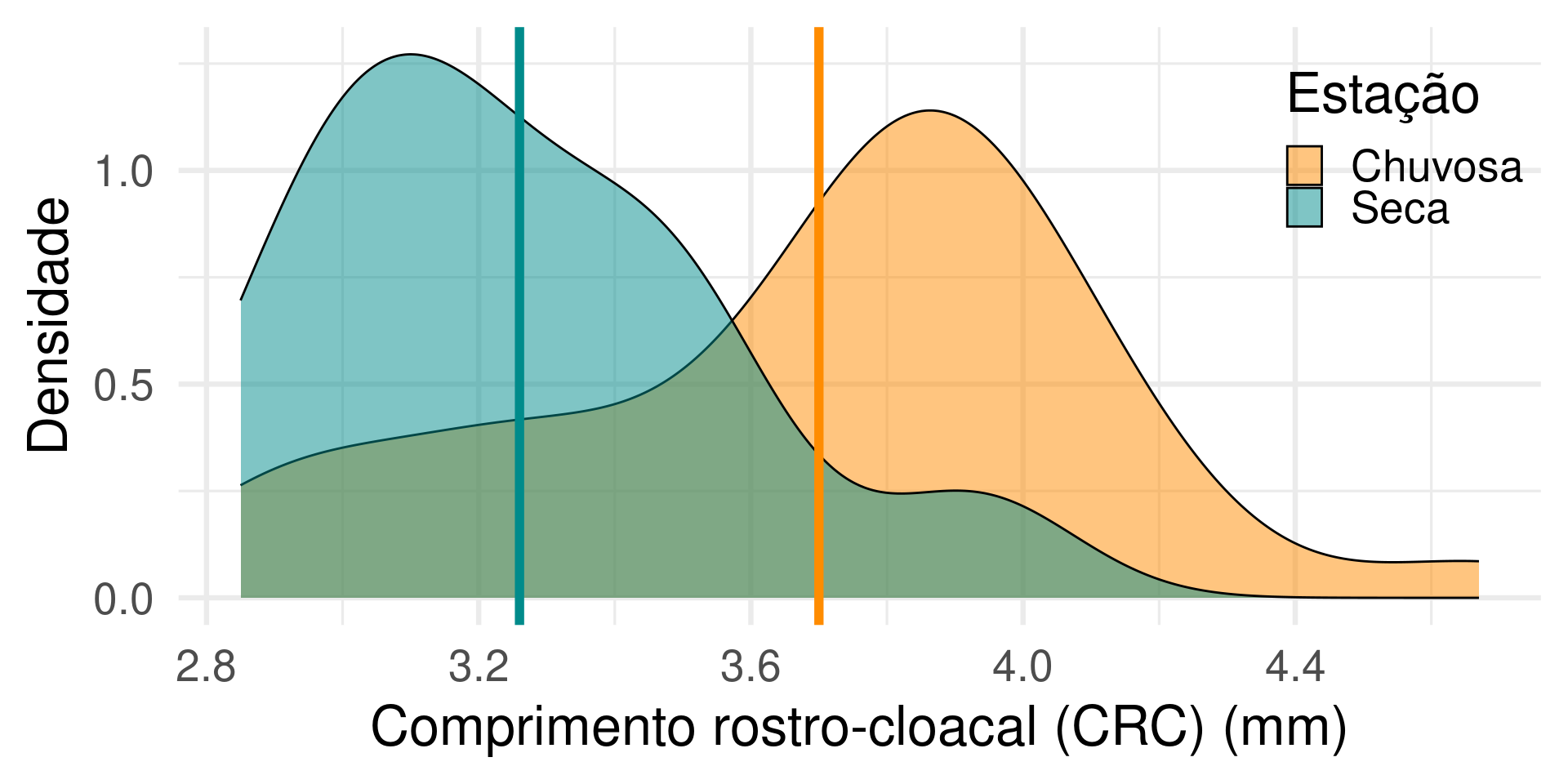
Teste t para duas amostras indep.

Independent-samples t test

## Teste de normalidade dos residuos - H0: distribuicao dos residuos é normal
residuos <- residuals(lm(CRC ~ Estacao, data = teste_t_var_igual))
shapiro.test(residuos)

    Shapiro-Wilk normality test

data:  residuos
W = 0.98307, p-value = 0.6746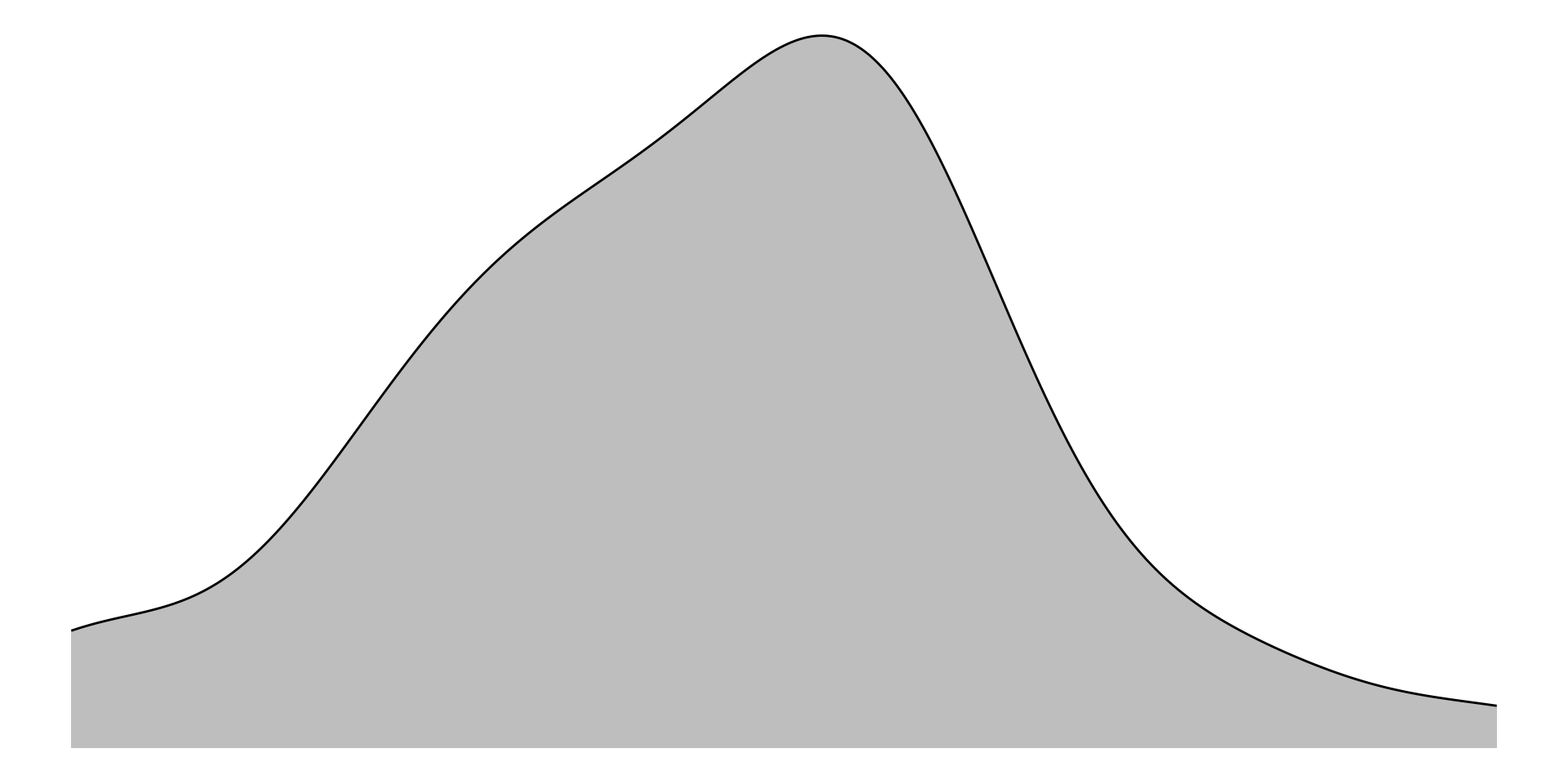

Teste t para duas amostras indep.

Independent-samples t test

## Teste de homogeneidade de variancia - H0: variancia e homogenea
car::leveneTest(CRC ~ as.factor(Estacao), data = teste_t_var_igual)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1  1.1677 0.2852
      49               

Teste t para duas amostras indep.

Independent-samples t test

## Análise Teste T 
t.test(CRC ~ Estacao, data = teste_t_var_igual, var.equal = TRUE)

    Two Sample t-test

data:  CRC by Estacao
t = 4.1524, df = 49, p-value = 0.000131
alternative hypothesis: true difference in means between group Chuvosa and group Seca is not equal to 0
95 percent confidence interval:
 0.2242132 0.6447619
sample estimates:
mean in group Chuvosa    mean in group Seca 
             3.695357              3.260870 

Teste t para duas amostras indep.

Independent-samples t test

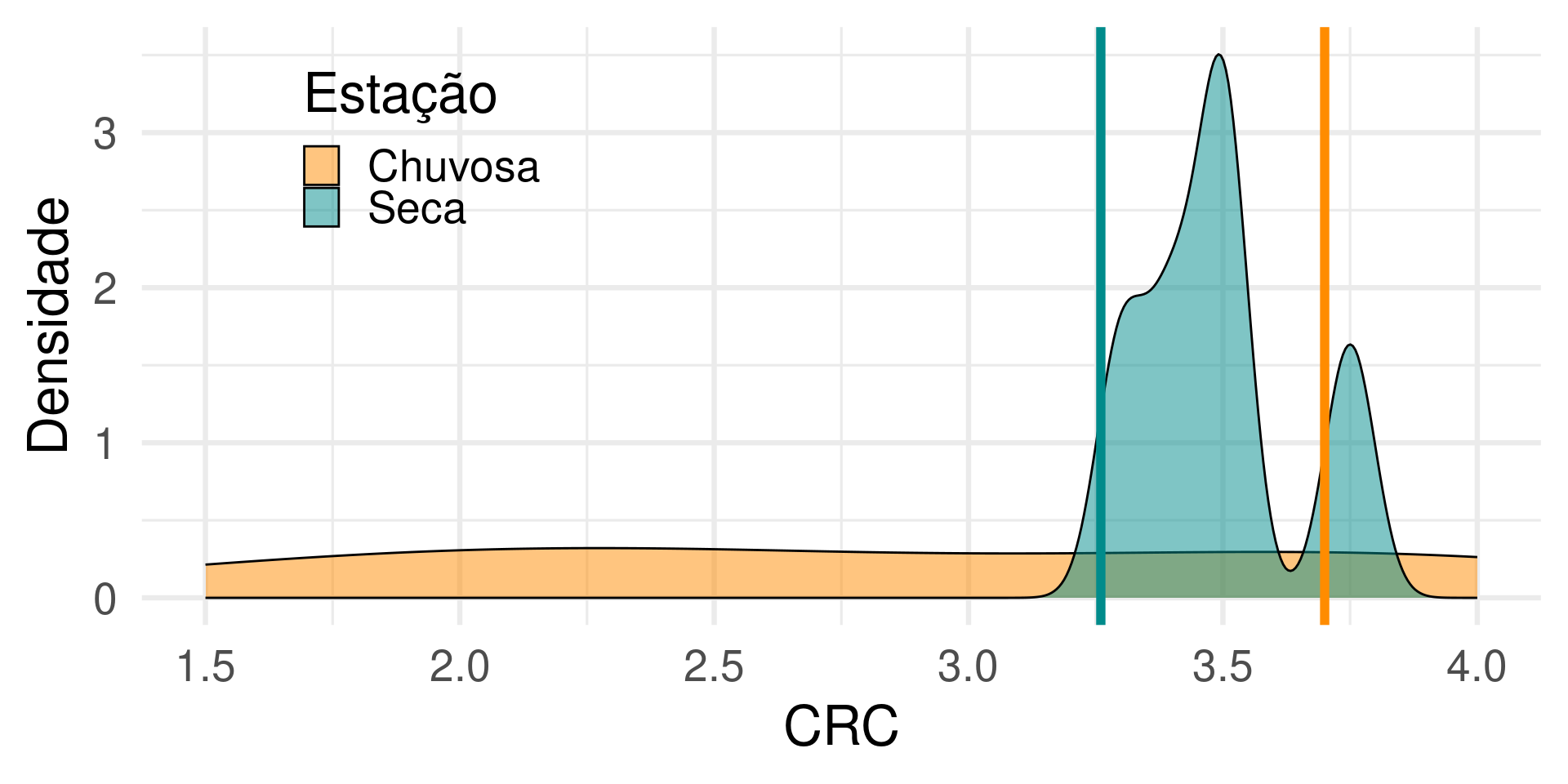
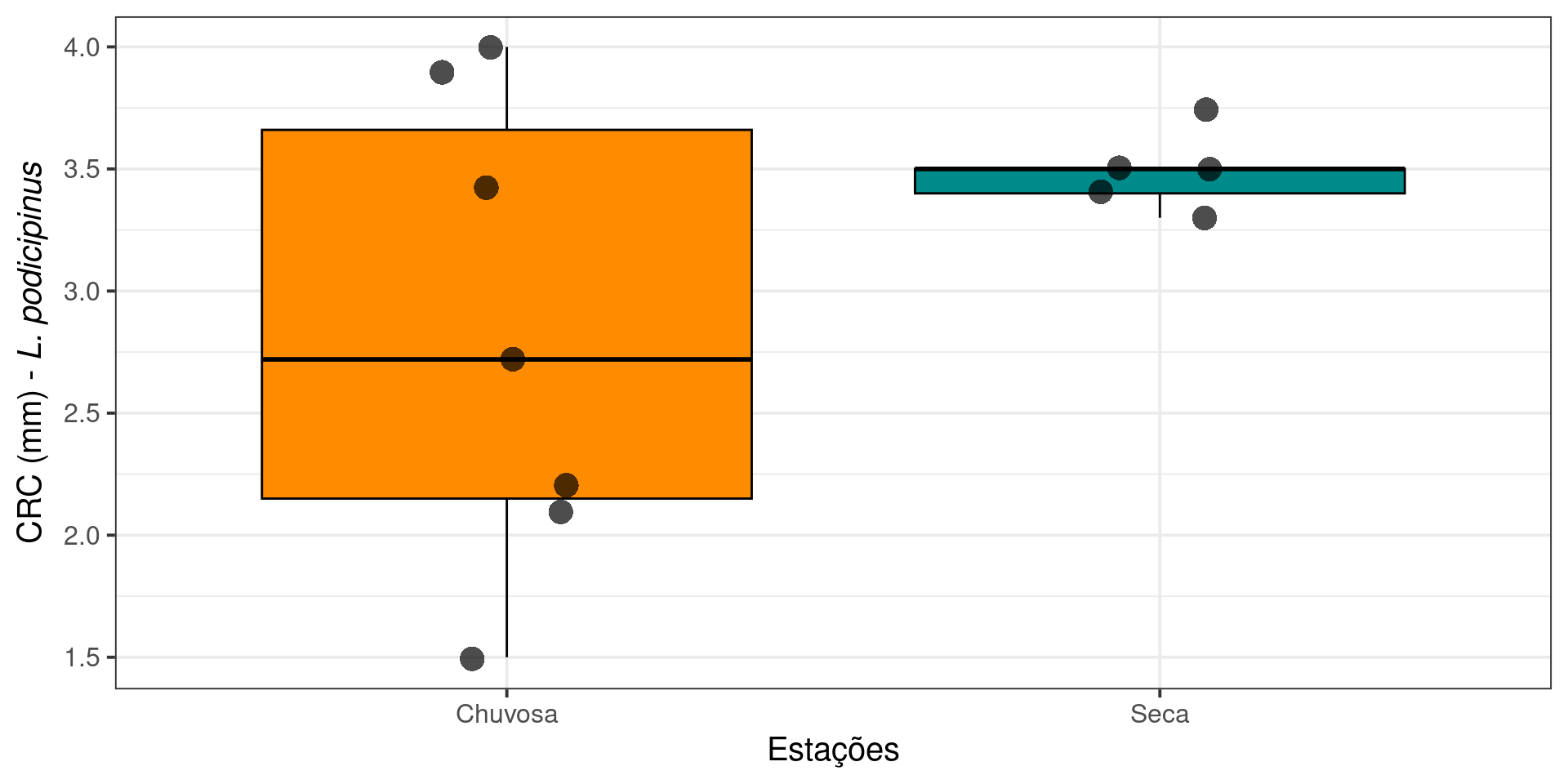
Leptodactylus podicipinus

Comprimento rostro-cloacal (CRC)

Teste t para duas amostras indep.

Independent-samples t test

Estacao	mean	sd
Chuvosa	2.83	0.96
Seca	3.49	0.17

Teste t para duas amostras indep.

Independent-samples t test

## Teste de normalidade dos residuos - H0: distribuicao dos residuos e normal
residuos <- residuals(lm(CRC ~ Estacao, data = teste_t_var_diferente))
shapiro.test(residuos)

    Shapiro-Wilk normality test

data:  residuos
W = 0.96272, p-value = 0.8219

Teste t para duas amostras indep.

Independent-samples t test

## Teste de homogeneidade de variancia - H0: variancia e homogenea
car::leveneTest(CRC ~ as.factor(Estacao), data = teste_t_var_diferente)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value  Pr(>F)  
group  1  9.8527 0.01053 *
      10                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Teste t para duas amostras indep.

Independent-samples t test

## Análise Teste T 
t.test(CRC ~ Estacao, data = teste_t_var_diferente, var.equal = TRUE)

    Two Sample t-test

data:  CRC by Estacao
t = -1.4853, df = 10, p-value = 0.1683
alternative hypothesis: true difference in means between group Chuvosa and group Seca is not equal to 0
95 percent confidence interval:
 -1.6393804  0.3279518
sample estimates:
mean in group Chuvosa    mean in group Seca 
             2.834286              3.490000 

Teste t para duas amostras indep.

Independent-samples t test

## Análise Teste T 
t.test(CRC ~ Estacao, data = teste_t_var_diferente, var.equal = FALSE)

    Welch Two Sample t-test

data:  CRC by Estacao
t = -1.7633, df = 6.4998, p-value = 0.1245
alternative hypothesis: true difference in means between group Chuvosa and group Seca is not equal to 0
95 percent confidence interval:
 -1.5489301  0.2375016
sample estimates:
mean in group Chuvosa    mean in group Seca 
             2.834286              3.490000 

Teste t para duas amostras indep.

Independent-samples t test

Teste t para duas amostras indep.

Conclusão

• Os machos de P. nattereri coletados na estação chuvosa foram em média 0,43 mm maiores do que os machos coletados na estação seca (t49 = 4,15, P < 0,001)

• As fêmeas de L. podicipinus coletadas na estação chuvosa não são maiores do que as fêmeas coletadas na estação seca, apesar de possuírem maior variância, o que pode ser biologicamente interessante

Teste t

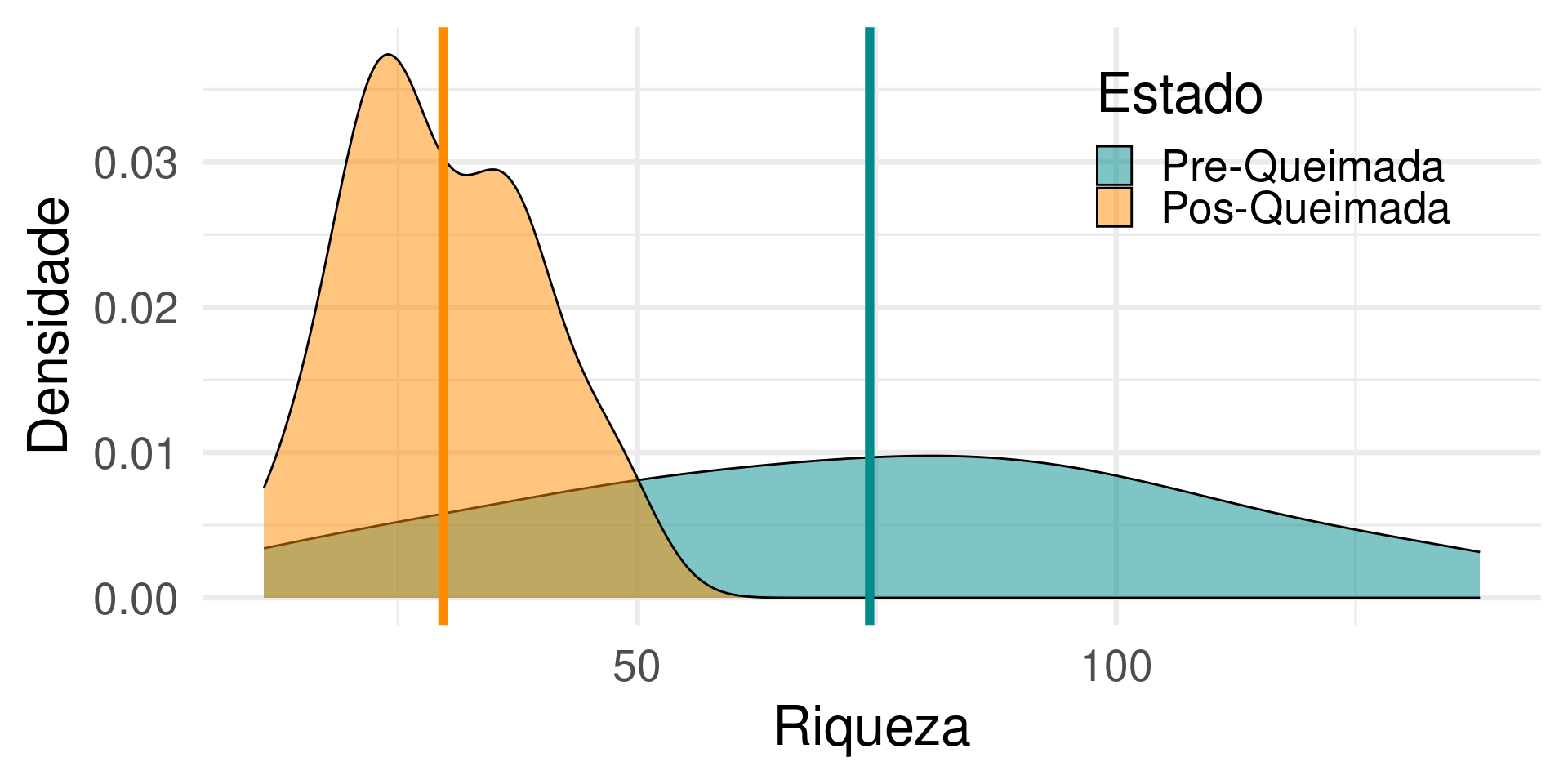
Área queimada

Número de espécies de artrópodes

Teste t para duas amostras pareadas

Paired-samples t test

Estado	mean	sd
Pre-Queimada	74.26	35.16
Pos-Queimada	29.70	9.71

Teste t para duas amostras indep.

Paired-samples t test

## Teste de normalidade dos residuos - H0: é normal
residuos <- residuals(lm(Riqueza ~ Estado, data = teste_t_pareado))
shapiro.test(residuos)

    Shapiro-Wilk normality test

data:  residuos
W = 0.96471, p-value = 0.1121

Teste t para duas amostras indep.

Paired-samples t test

## Teste de homogeneidade de variancia - H0: tem homogeneidade
car::leveneTest(Riqueza ~ as.factor(Estado), data = teste_t_pareado)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value   Pr(>F)    
group  1  26.138 4.64e-06 ***
      52                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Teste t para duas amostras indep.

Paired-samples t test

## Análise Teste T Pareado
t.test(Riqueza ~ Estado, paired = TRUE, data = teste_t_pareado)

    Paired t-test

data:  Riqueza by Estado
t = -7.5788, df = 26, p-value = 4.803e-08
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
 -56.63994 -32.47117
sample estimates:
mean difference 
      -44.55556 

Teste t para duas amostras indep.

Paired-samples t test

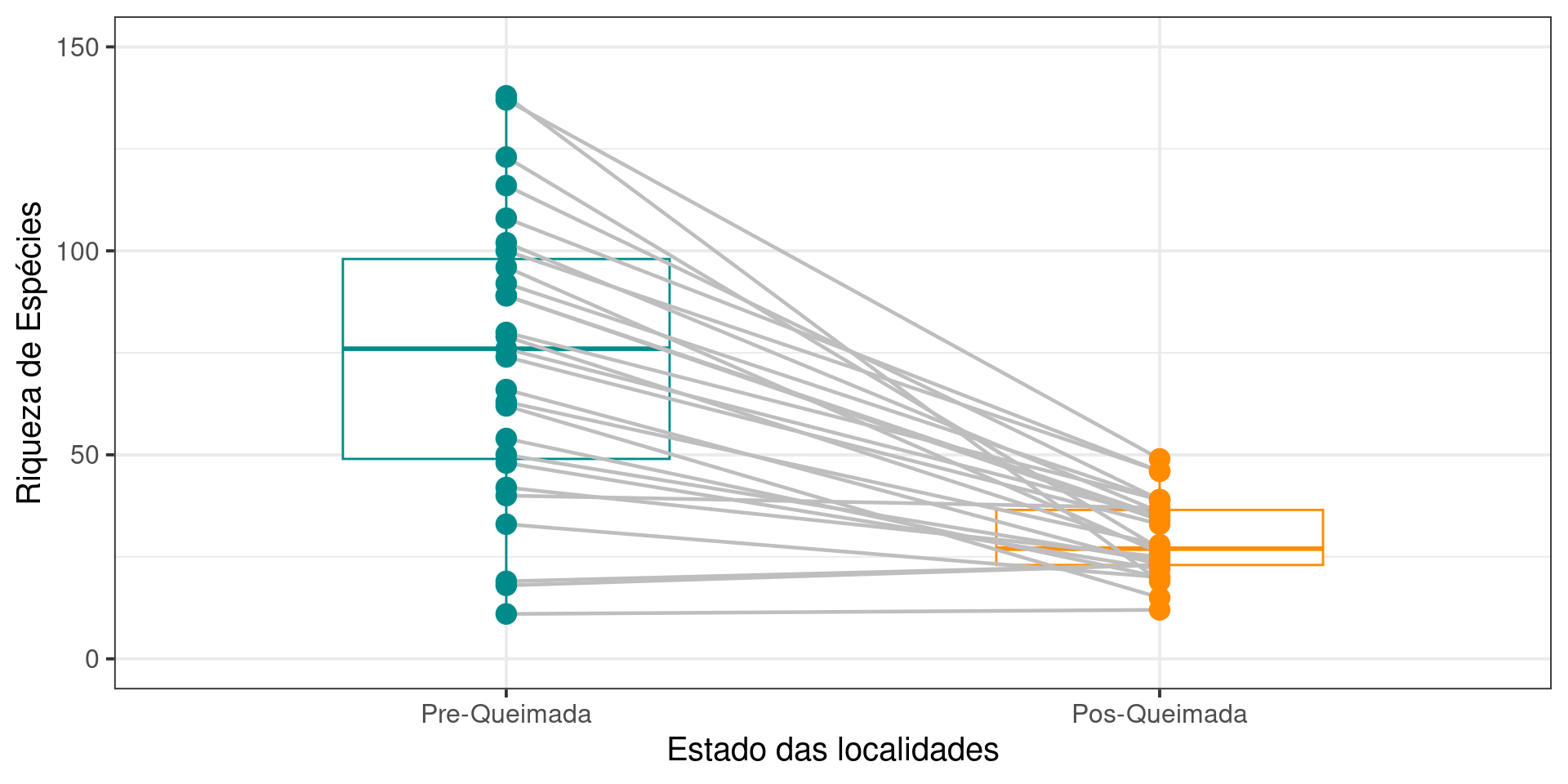
Teste t para duas amostras indep.

Conclusão

Os resultados mostram que as localidades após as queimadas apresentam em média 44,5 espécies de artrópodes a menos do que antes das queimadas

Dúvidas?

Resumindo

Resumindo

• Linguagem R

• Análise Exploratória de Dados (AED): medidas-resumo, tabelas e gráficos

• Análise de dados univariados

• Pergunta e hipótese

• Hipótese ecológica e hipótese estatística

• População e amostra

• Parâmetro e estatística (estimador)

• Média, variância, desvio padrão, erro padrão

• Inferência estatística: intervalo de confiança e teste de hipóteses

• Distribuição z e t e valor de p

• Teste t para uma amostra

• Teste t para duas amostras indep.

• Teste t para duas amostras pareadas

Material de estudo

Material de estudo

• Análises Ecológicas no R (2022)

• Princípios de Estatística em Ecologia (2010)

• Estatística Básica (2017)

• Estatística e Ciência de Dados (2022)

• Analysing Ecological Data (2007)

• Ecological Statistics: Contemporary theory and application (2015)

• Fernanda Peres

Muito obrigado!

Agradecimentos:

• Fernanda Peres
• Prof. Tadeu Siqueira
• Prof. Milton Cezar Ribeiro
• Fapesp #2022/01899-6

Contato: